Learning the hypotheses space from data through a U-curve algorithm: a statistically consistent complexity regularizer for Model Selection
Paper and Code
Sep 08, 2021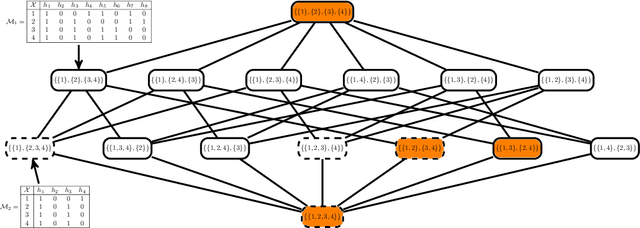
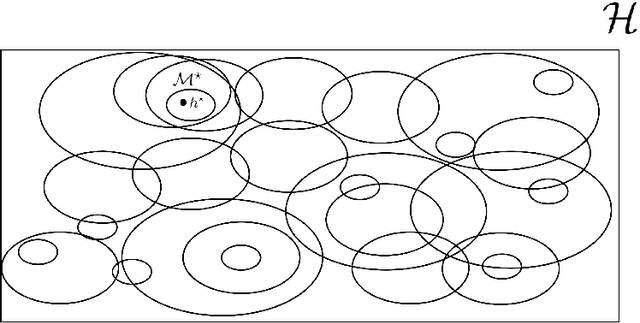
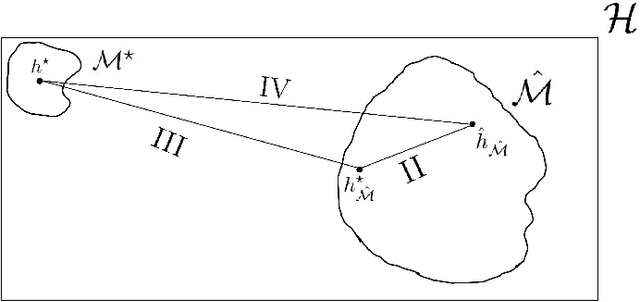
This paper proposes a data-driven systematic, consistent and non-exhaustive approach to Model Selection, that is an extension of the classical agnostic PAC learning model. In this approach, learning problems are modeled not only by a hypothesis space $\mathcal{H}$, but also by a Learning Space $\mathbb{L}(\mathcal{H})$, a poset of subspaces of $\mathcal{H}$, which covers $\mathcal{H}$ and satisfies a property regarding the VC dimension of related subspaces, that is a suitable algebraic search space for Model Selection algorithms. Our main contributions are a data-driven general learning algorithm to perform regularized Model Selection on $\mathbb{L}(\mathcal{H})$ and a framework under which one can, theoretically, better estimate a target hypothesis with a given sample size by properly modeling $\mathbb{L}(\mathcal{H})$ and employing high computational power. A remarkable consequence of this approach are conditions under which a non-exhaustive search of $\mathbb{L}(\mathcal{H})$ can return an optimal solution. The results of this paper lead to a practical property of Machine Learning, that the lack of experimental data may be mitigated by a high computational capacity. In a context of continuous popularization of computational power, this property may help understand why Machine Learning has become so important, even where data is expensive and hard to get.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge