Generalized Resubstitution for Regression Error Estimation

We propose generalized resubstitution error estimators for regression, a broad family of estimators, each corresponding to a choice of empirical probability measures and loss function. The usual sum of squares criterion is a special case corresponding to the standard empirical probability measure and the quadratic loss. Other choices of empirical probability measure lead to more general estimators with superior bias and variance properties. We prove that these error estimators are consistent under broad assumptions. In addition, procedures for choosing the empirical measure based on the method of moments and maximum pseudo-likelihood are proposed and investigated. Detailed experimental results using polynomial regression demonstrate empirically the superior finite-sample bias and variance properties of the proposed estimators. The R code for the experiments is provided.

The Lattice Overparametrization Paradigm for the Machine Learning of Lattice Operators

The machine learning of lattice operators has three possible bottlenecks. From a statistical standpoint, it is necessary to design a constrained class of operators based on prior information with low bias, and low complexity relative to the sample size. From a computational perspective, there should be an efficient algorithm to minimize an empirical error over the class. From an understanding point of view, the properties of the learned operator need to be derived, so its behavior can be theoretically understood. The statistical bottleneck can be overcome due to the rich literature about the representation of lattice operators, but there is no general learning algorithm for them. In this paper, we discuss a learning paradigm in which, by overparametrizing a class via elements in a lattice, an algorithm for minimizing functions in a lattice is applied to learn. We present the stochastic lattice gradient descent algorithm as a general algorithm to learn on constrained classes of operators as long as a lattice overparametrization of it is fixed, and we discuss previous works which are proves of concept. Moreover, if there are algorithms to compute the basis of an operator from its overparametrization, then its properties can be deduced and the understanding bottleneck is also overcome. This learning paradigm has three properties that modern methods based on neural networks lack: control, transparency and interpretability. Nowadays, there is an increasing demand for methods with these characteristics, and we believe that mathematical morphology is in a unique position to supply them. The lattice overparametrization paradigm could be a missing piece for it to achieve its full potential within modern machine learning.

An Algorithm to Train Unrestricted Sequential Discrete Morphological Neural Networks

With the advent of deep learning, there have been attempts to insert mathematical morphology (MM) operators into convolutional neural networks (CNN), and the most successful endeavor to date has been the morphological neural networks (MNN). Although MNN have performed better than CNN in solving some problems, they inherit their black-box nature. Furthermore, in the case of binary images, they are approximations, which loose the Boolean lattice structure of MM operators and, thus, it is not possible to represent a specific class of W-operators with desired properties. In a recent work, we proposed the Discrete Morphological Neural Networks (DMNN) for binary image transformation to represent specific classes of W-operators and estimate them via machine learning. We also proposed a stochastic lattice gradient descent algorithm (SLGDA) to learn the parameters of Canonical Discrete Morphological Neural Networks (CDMNN), whose architecture is composed only of operators that can be decomposed as the supremum, infimum, and complement of erosions and dilations. In this paper, we propose an algorithm to learn unrestricted sequential DMNN (USDMNN), whose architecture is given by the composition of general W-operators. We consider the representation of a W-operator by its characteristic Boolean function, and then learn it via a SLGDA in the Boolean lattice of functions. Although both the CDMNN and USDMNN have the Boolean lattice structure, USDMNN are not as dependent on prior information about the problem at hand, and may be more suitable in instances in which the practitioner does not have strong domain knowledge. We illustrate the algorithm in a practical example.

Discrete Morphological Neural Networks

A classical approach to designing binary image operators is Mathematical Morphology (MM). We propose the Discrete Morphological Neural Networks (DMNN) for binary image analysis to represent W-operators and estimate them via machine learning. A DMNN architecture, which is represented by a Morphological Computational Graph, is designed as in the classical heuristic design of morphological operators, in which the designer should combine a set of MM operators and Boolean operations based on prior information and theoretical knowledge. Then, once the architecture is fixed, instead of adjusting its parameters (i.e., structural elements or maximal intervals) by hand, we propose a lattice gradient descent algorithm (LGDA) to train these parameters based on a sample of input and output images under the usual machine learning approach. We also propose a stochastic version of the LGDA that is more efficient, is scalable and can obtain small error in practical problems. The class represented by a DMNN can be quite general or specialized according to expected properties of the target operator, i.e., prior information, and the semantic expressed by algebraic properties of classes of operators is a differential relative to other methods. The main contribution of this paper is the merger of the two main paradigms for designing morphological operators: classical heuristic design and automatic design via machine learning. Thus, conciliating classical heuristic morphological operator design with machine learning. We apply the DMNN to recognize the boundary of digits with noise, and we discuss many topics for future research.

Distribution-free Deviation Bounds of Learning via Model Selection with Cross-validation Risk Estimation

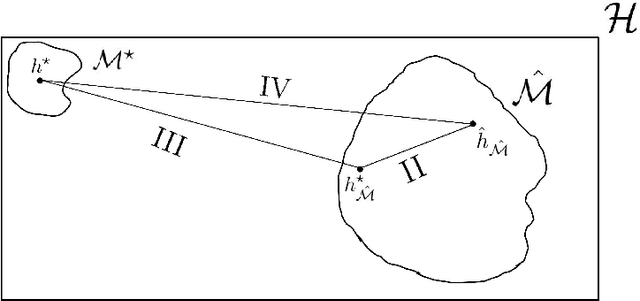
Cross-validation techniques for risk estimation and model selection are widely used in statistics and machine learning. However, the understanding of the theoretical properties of learning via model selection with cross-validation risk estimation is quite low in face of its widespread use. In this context, this paper presents learning via model selection with cross-validation risk estimation as a general systematic learning framework within classical statistical learning theory and establishes distribution-free deviation bounds in terms of VC dimension, giving detailed proofs of the results and considering both bounded and unbounded loss functions. We also deduce conditions under which the deviation bounds of learning via model selection are tighter than that of learning via empirical risk minimization in the whole hypotheses space, supporting the better performance of model selection frameworks observed empirically in some instances.

The role of prior information and computational power in Machine Learning

Science consists on conceiving hypotheses, confronting them with empirical evidence, and keeping only hypotheses which have not yet been falsified. Under deductive reasoning they are conceived in view of a theory and confronted with empirical evidence in an attempt to falsify it, and under inductive reasoning they are conceived based on observation, confronted with empirical evidence and a theory is established based on the not falsified hypotheses. When the hypotheses testing can be performed with quantitative data, the confrontation can be achieved with Machine Learning methods, whose quality is highly dependent on the hypotheses' complexity, hence on the proper insertion of prior information into the set of hypotheses seeking to decrease its complexity without loosing good hypotheses. However, Machine Learning tools have been applied under the pragmatic view of instrumentalism, which is concerned only with the performance of the methods and not with the understanding of their behavior, leading to methods which are not fully understood. In this context, we discuss how prior information and computational power can be employed to solve a learning problem, but while prior information and a careful design of the hypotheses space has as advantage the interpretability of the results, employing high computational power has the advantage of a higher performance. We discuss why learning methods which combine both should work better from an understanding and performance perspective, arguing in favor of basic theoretical research on Machine Learning, in special about how properties of classifiers may be identified in parameters of modern learning models.

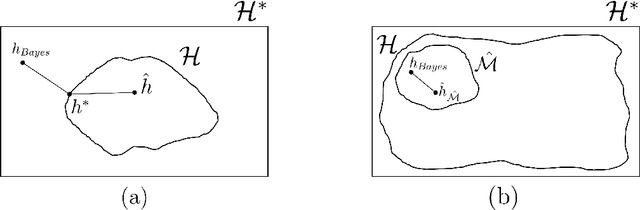
Learning the hypotheses space from data through a U-curve algorithm: a statistically consistent complexity regularizer for Model Selection

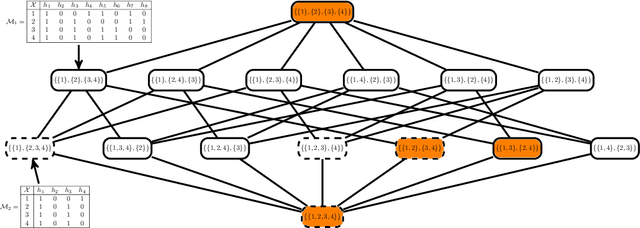
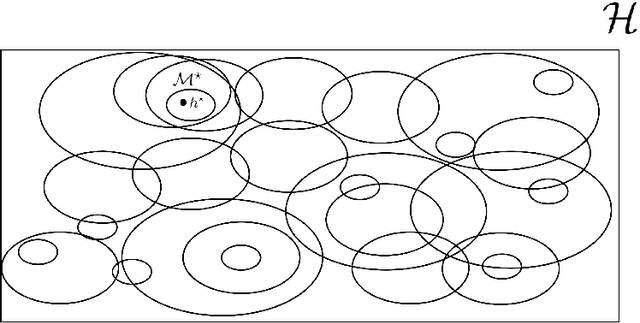
This paper proposes a data-driven systematic, consistent and non-exhaustive approach to Model Selection, that is an extension of the classical agnostic PAC learning model. In this approach, learning problems are modeled not only by a hypothesis space $\mathcal{H}$, but also by a Learning Space $\mathbb{L}(\mathcal{H})$, a poset of subspaces of $\mathcal{H}$, which covers $\mathcal{H}$ and satisfies a property regarding the VC dimension of related subspaces, that is a suitable algebraic search space for Model Selection algorithms. Our main contributions are a data-driven general learning algorithm to perform regularized Model Selection on $\mathbb{L}(\mathcal{H})$ and a framework under which one can, theoretically, better estimate a target hypothesis with a given sample size by properly modeling $\mathbb{L}(\mathcal{H})$ and employing high computational power. A remarkable consequence of this approach are conditions under which a non-exhaustive search of $\mathbb{L}(\mathcal{H})$ can return an optimal solution. The results of this paper lead to a practical property of Machine Learning, that the lack of experimental data may be mitigated by a high computational capacity. In a context of continuous popularization of computational power, this property may help understand why Machine Learning has become so important, even where data is expensive and hard to get.

Robust parameter estimation in dynamical systems via Statistical Learning with an application to epidemiological models

We propose a robust parameter estimation method for dynamical systems based on Statistical Learning techniques which aims to estimate a set of parameters that well fit the dynamics in order to obtain robust evidences about the qualitative behaviour of its trajectory. The method is quite general and flexible, since it dos not rely on any specific property of the dynamical system, and represents a mathematical formalisation of the procedure consisting of sampling and testing parameters, in which evolutions generated by candidate parameters are tested against observed data to assess goodness-of-fit. The Statistical Learning framework introduces a mathematically rigorous scheme to this general approach for parameter estimation, adding to the great field of parameter estimation in dynamical systems. The method is specially useful for estimating parameters in epidemiological compartmental models. We illustrate it in simulated and real data about COVID-19 spread in the US in order to assess qualitatively the peak of deaths by the disease.

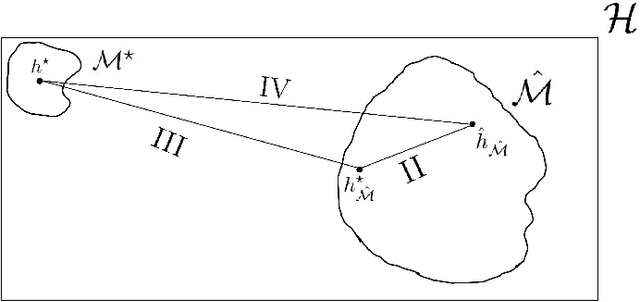
Learning the Hypotheses Space from data Part II: Convergence and Feasibility

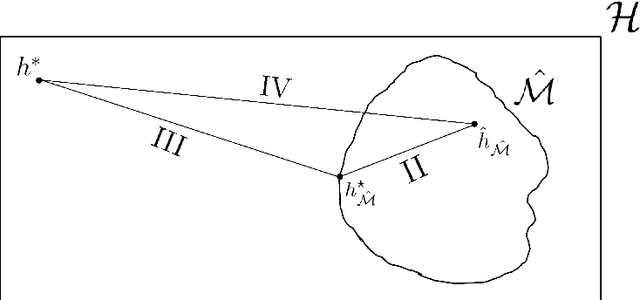
In part \textit{I} we proposed a structure for a general Hypotheses Space $\mathcal{H}$, the Learning Space $\mathbb{L}(\mathcal{H})$, which can be employed to avoid \textit{overfitting} when estimating in a complex space with relative shortage of examples. Also, we presented the U-curve property, which can be taken advantage of in order to select a Hypotheses Space without exhaustively searching $\mathbb{L}(\mathcal{H})$. In this paper, we carry further our agenda, by showing the consistency of a model selection framework based on Learning Spaces, in which one selects from data the Hypotheses Space on which to learn. The method developed in this paper adds to the state-of-the-art in model selection, by extending Vapnik-Chervonenkis Theory to \textit{random} Hypotheses Spaces, i.e., Hypotheses Spaces learned from data. In this framework, one estimates a random subspace $\hat{\mathcal{M}} \in \mathbb{L}(\mathcal{H})$ which converges with probability one to a target Hypotheses Space $\mathcal{M}^{\star} \in \mathbb{L}(\mathcal{H})$ with desired properties. As the convergence implies asymptotic unbiased estimators, we have a consistent framework for model selection, showing that it is feasible to learn the Hypotheses Space from data. Furthermore, we show that the generalization errors of learning on $\hat{\mathcal{M}}$ are lesser than those we commit when learning on $\mathcal{H}$, so it is more efficient to learn on a subspace learned from data.

Learning the Hypotheses Space from data Part I: Learning Space and U-curve Property

The agnostic PAC learning model consists of: a Hypothesis Space $\mathcal{H}$, a probability distribution $P$, a sample complexity function $m_{\mathcal{H}}(\epsilon,\delta): [0,1]^{2} \mapsto \mathbb{Z}_{+}$ of precision $\epsilon$ and confidence $1 - \delta$, a finite i.i.d. sample $\mathcal{D}_{N}$, a cost function $\ell$ and a learning algorithm $\mathbb{A}(\mathcal{H},\mathcal{D}_{N})$, which estimates $\hat{h} \in \mathcal{H}$ that approximates a target function $h^{\star} \in \mathcal{H}$ seeking to minimize out-of-sample error. In this model, prior information is represented by $\mathcal{H}$ and $\ell$, while problem solution is performed through their instantiation in several applied learning models, with specific algebraic structures for $\mathcal{H}$ and corresponding learning algorithms. However, these applied models use additional important concepts not covered by the classic PAC learning theory: model selection and regularization. This paper presents an extension of this model which covers these concepts. The main principle added is the selection, based solely on data, of a subspace of $\mathcal{H}$ with a VC-dimension compatible with the available sample. In order to formalize this principle, the concept of Learning Space $\mathbb{L}(\mathcal{H})$, which is a poset of subsets of $\mathcal{H}$ that covers $\mathcal{H}$ and satisfies a property regarding the VC dimension of related subspaces, is presented as the natural search space for model selection algorithms. A remarkable result obtained on this new framework are conditions on $\mathbb{L}(\mathcal{H})$ and $\ell$ that lead to estimated out-of-sample error surfaces, which are true U-curves on $\mathbb{L}(\mathcal{H})$ chains, enabling a more efficient search on $\mathbb{L}(\mathcal{H})$. Hence, in this new framework, the U-curve optimization problem becomes a natural component of model selection algorithms.