Learning the Hypotheses Space from data Part II: Convergence and Feasibility
Paper and Code
Jan 30, 2020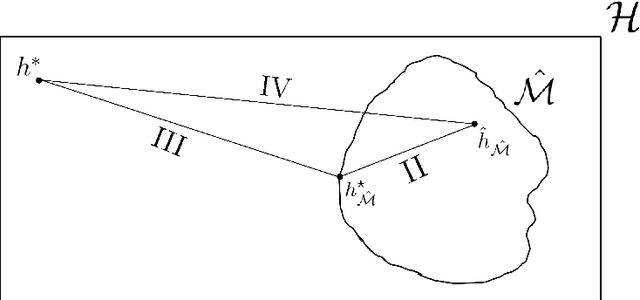
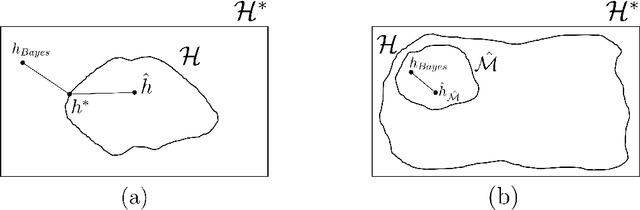
In part \textit{I} we proposed a structure for a general Hypotheses Space $\mathcal{H}$, the Learning Space $\mathbb{L}(\mathcal{H})$, which can be employed to avoid \textit{overfitting} when estimating in a complex space with relative shortage of examples. Also, we presented the U-curve property, which can be taken advantage of in order to select a Hypotheses Space without exhaustively searching $\mathbb{L}(\mathcal{H})$. In this paper, we carry further our agenda, by showing the consistency of a model selection framework based on Learning Spaces, in which one selects from data the Hypotheses Space on which to learn. The method developed in this paper adds to the state-of-the-art in model selection, by extending Vapnik-Chervonenkis Theory to \textit{random} Hypotheses Spaces, i.e., Hypotheses Spaces learned from data. In this framework, one estimates a random subspace $\hat{\mathcal{M}} \in \mathbb{L}(\mathcal{H})$ which converges with probability one to a target Hypotheses Space $\mathcal{M}^{\star} \in \mathbb{L}(\mathcal{H})$ with desired properties. As the convergence implies asymptotic unbiased estimators, we have a consistent framework for model selection, showing that it is feasible to learn the Hypotheses Space from data. Furthermore, we show that the generalization errors of learning on $\hat{\mathcal{M}}$ are lesser than those we commit when learning on $\mathcal{H}$, so it is more efficient to learn on a subspace learned from data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge