Learning the Hypotheses Space from data Part I: Learning Space and U-curve Property

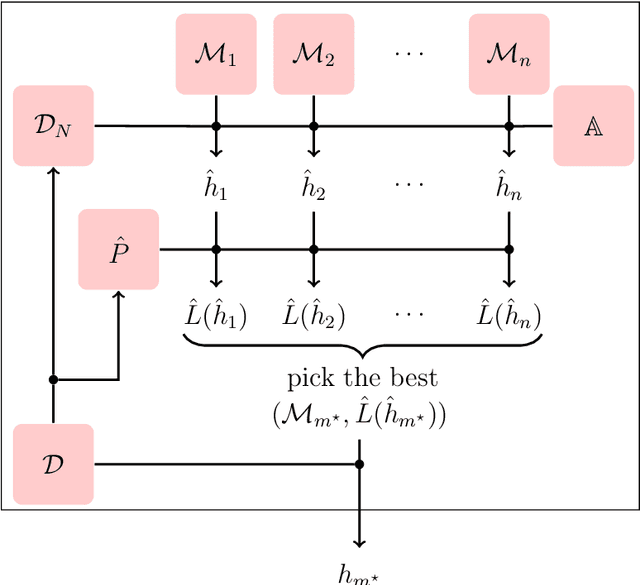
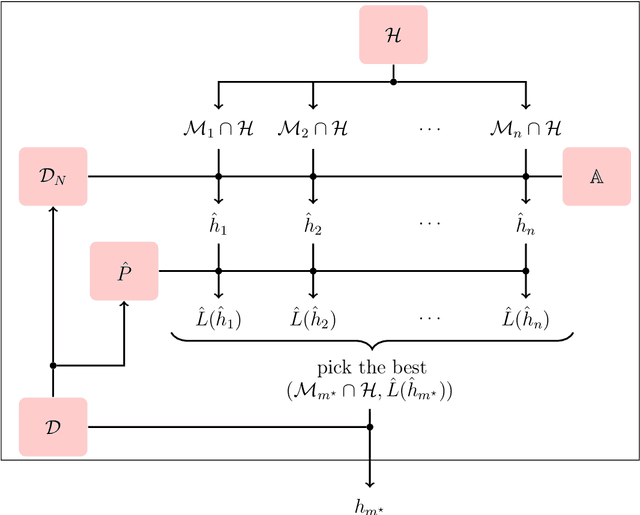
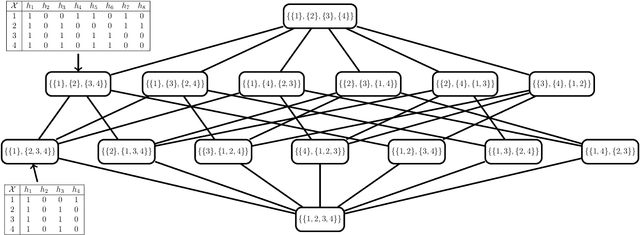
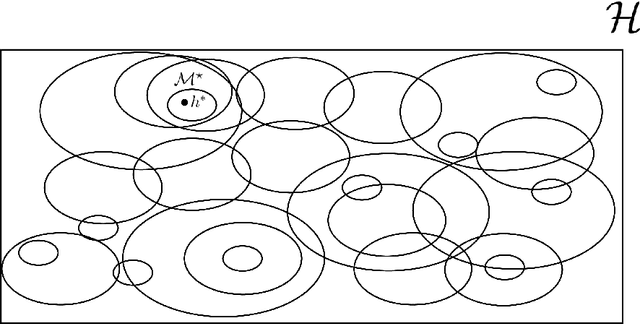
The agnostic PAC learning model consists of: a Hypothesis Space $\mathcal{H}$, a probability distribution $P$, a sample complexity function $m_{\mathcal{H}}(\epsilon,\delta): [0,1]^{2} \mapsto \mathbb{Z}_{+}$ of precision $\epsilon$ and confidence $1 - \delta$, a finite i.i.d. sample $\mathcal{D}_{N}$, a cost function $\ell$ and a learning algorithm $\mathbb{A}(\mathcal{H},\mathcal{D}_{N})$, which estimates $\hat{h} \in \mathcal{H}$ that approximates a target function $h^{\star} \in \mathcal{H}$ seeking to minimize out-of-sample error. In this model, prior information is represented by $\mathcal{H}$ and $\ell$, while problem solution is performed through their instantiation in several applied learning models, with specific algebraic structures for $\mathcal{H}$ and corresponding learning algorithms. However, these applied models use additional important concepts not covered by the classic PAC learning theory: model selection and regularization. This paper presents an extension of this model which covers these concepts. The main principle added is the selection, based solely on data, of a subspace of $\mathcal{H}$ with a VC-dimension compatible with the available sample. In order to formalize this principle, the concept of Learning Space $\mathbb{L}(\mathcal{H})$, which is a poset of subsets of $\mathcal{H}$ that covers $\mathcal{H}$ and satisfies a property regarding the VC dimension of related subspaces, is presented as the natural search space for model selection algorithms. A remarkable result obtained on this new framework are conditions on $\mathbb{L}(\mathcal{H})$ and $\ell$ that lead to estimated out-of-sample error surfaces, which are true U-curves on $\mathbb{L}(\mathcal{H})$ chains, enabling a more efficient search on $\mathbb{L}(\mathcal{H})$. Hence, in this new framework, the U-curve optimization problem becomes a natural component of model selection algorithms.