Feature Selection based on the Local Lift Dependence Scale
Paper and Code
Dec 18, 2017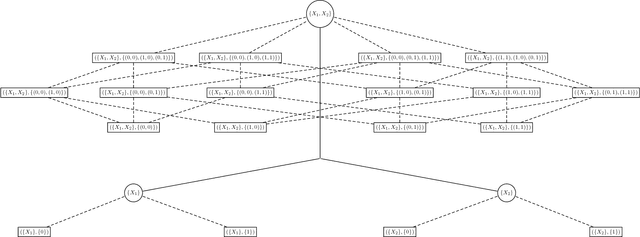
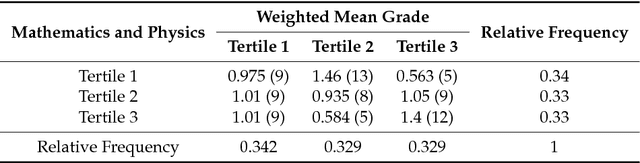
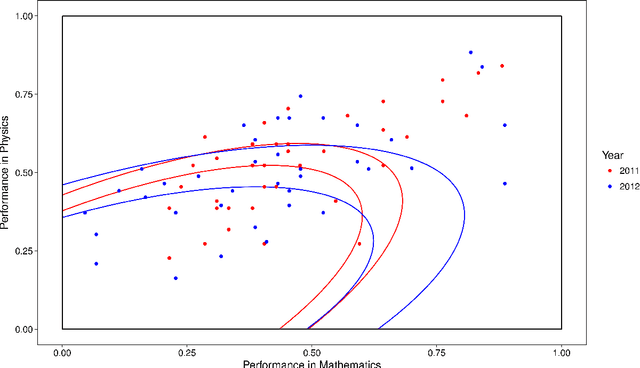
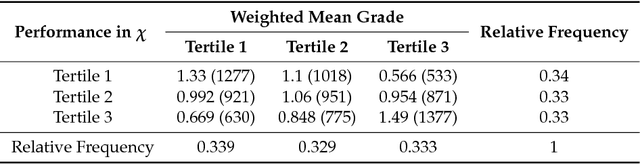
This paper uses a classical approach to feature selection: minimization of a cost function applied on estimated joint distributions. However, the search space in which such minimization is performed is extended. In the original formulation, the search space is the Boolean lattice of features sets (BLFS), while, in the present formulation, it is a collection of Boolean lattices of ordered pairs (features, associated value) (CBLOP), indexed by the elements of the BLFS. In this approach, we may not only select the features that are most related to a variable Y, but also select the values of the features that most influence the variable or that are most prone to have a specific value of Y. A local formulation of Shanon's mutual information is applied on a CBLOP to select features, namely, the Local Lift Dependence Scale, an scale for measuring variable dependence in multiple resolutions. The main contribution of this paper is to define and apply this local measure, which permits to analyse local properties of joint distributions that are neglected by the classical Shanon's global measure. The proposed approach is applied to a dataset consisting of student performances on a university entrance exam, as well as on undergraduate courses. The approach is also applied to two datasets of the UCI Machine Learning Repository.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge