The LogBarrier adversarial attack: making effective use of decision boundary information

Adversarial attacks for image classification are small perturbations to images that are designed to cause misclassification by a model. Adversarial attacks formally correspond to an optimization problem: find a minimum norm image perturbation, constrained to cause misclassification. A number of effective attacks have been developed. However, to date, no gradient-based attacks have used best practices from the optimization literature to solve this constrained minimization problem. We design a new untargeted attack, based on these best practices, using the established logarithmic barrier method. On average, our attack distance is similar or better than all state-of-the-art attacks on benchmark datasets (MNIST, CIFAR10, ImageNet-1K). In addition, our method performs significantly better on the most challenging images, those which normally require larger perturbations for misclassification. We employ the LogBarrier attack on several adversarially defended models, and show that it adversarially perturbs all images more efficiently than other attacks: the distance needed to perturb all images is significantly smaller with the LogBarrier attack than with other state-of-the-art attacks.

Empirical confidence estimates for classification by deep neural networks

How well can we estimate the probability that the classification, $C(f(x))$, predicted by a deep neural network is correct (or in the Top 5)? We consider the case of a classification neural network trained with the KL divergence which is assumed to generalize, as measured empirically by the test error and test loss. We present conditional probabilities for predictions based on the histogram of uncertainty metrics, which have a significant Bayes ratio. Previous work in this area includes Bayesian neural networks. Our metric is twice as predictive, based on the expected Bayes ratio, on ImageNet compared to our best tuned implementation of Bayesian dropout~\cite{gal2016dropout}. Our method uses just the softmax values and a stored histogram so it is essentially free to compute, compared to many times inference cost for Bayesian dropout.

Anomaly detection and classification for streaming data using PDEs

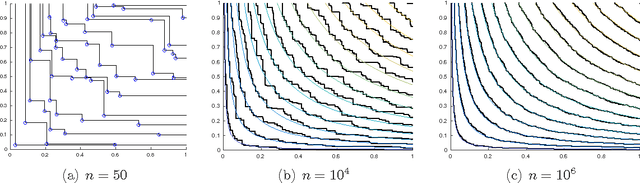
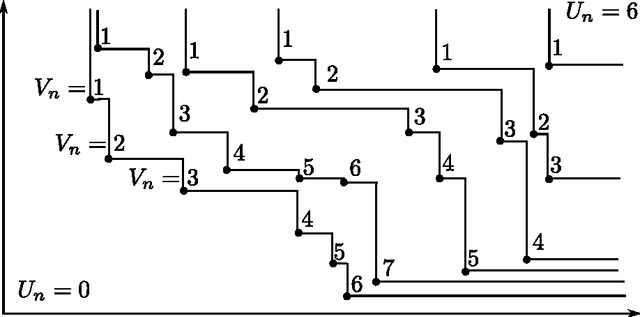
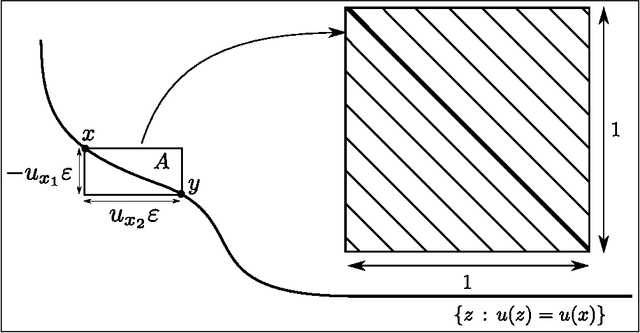
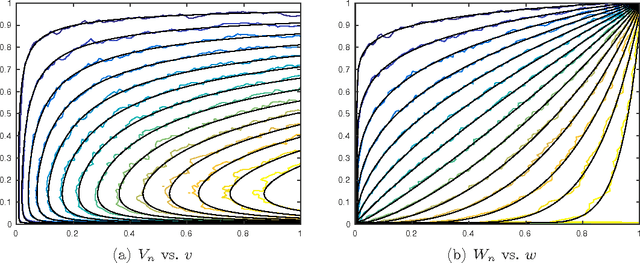
Nondominated sorting, also called Pareto Depth Analysis (PDA), is widely used in multi-objective optimization and has recently found important applications in multi-criteria anomaly detection. Recently, a partial differential equation (PDE) continuum limit was discovered for nondominated sorting leading to a very fast approximate sorting algorithm called PDE-based ranking. We propose in this paper a fast real-time streaming version of the PDA algorithm for anomaly detection that exploits the computational advantages of PDE continuum limits. Furthermore, we derive new PDE continuum limits for sorting points within their nondominated layers and show how the new PDEs can be used to classify anomalies based on which criterion was more significantly violated. We also prove statistical convergence rates for PDE-based ranking, and present the results of numerical experiments with both synthetic and real data.