Anomaly detection and classification for streaming data using PDEs

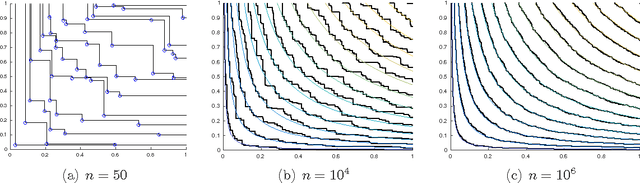
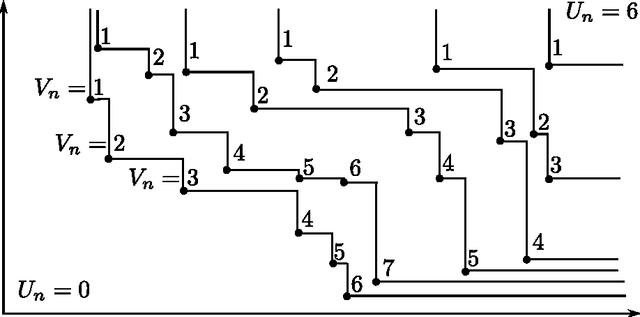
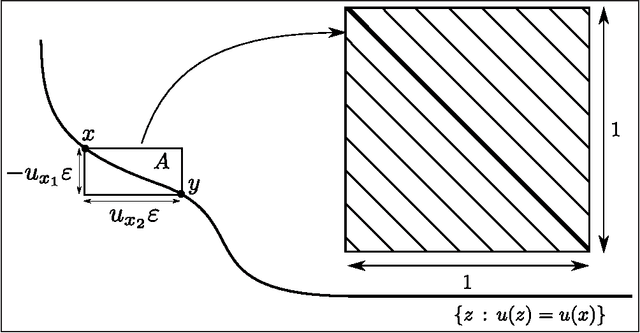
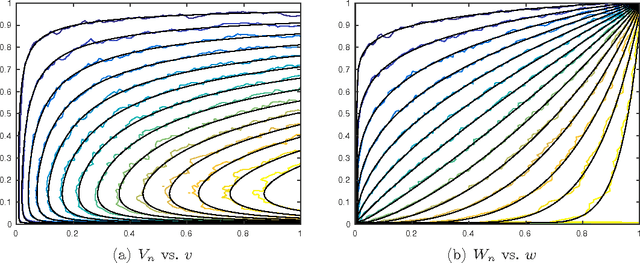
Nondominated sorting, also called Pareto Depth Analysis (PDA), is widely used in multi-objective optimization and has recently found important applications in multi-criteria anomaly detection. Recently, a partial differential equation (PDE) continuum limit was discovered for nondominated sorting leading to a very fast approximate sorting algorithm called PDE-based ranking. We propose in this paper a fast real-time streaming version of the PDA algorithm for anomaly detection that exploits the computational advantages of PDE continuum limits. Furthermore, we derive new PDE continuum limits for sorting points within their nondominated layers and show how the new PDEs can be used to classify anomalies based on which criterion was more significantly violated. We also prove statistical convergence rates for PDE-based ranking, and present the results of numerical experiments with both synthetic and real data.