Satyrn: A Platform for Analytics Augmented Generation

Large language models (LLMs) are capable of producing documents, and retrieval augmented generation (RAG) has shown itself to be a powerful method for improving accuracy without sacrificing fluency. However, not all information can be retrieved from text. We propose an approach that uses the analysis of structured data to generate fact sets that are used to guide generation in much the same way that retrieved documents are used in RAG. This analytics augmented generation (AAG) approach supports the ability to utilize standard analytic techniques to generate facts that are then converted to text and passed to an LLM. We present a neurosymbolic platform, Satyrn that leverages AAG to produce accurate, fluent, and coherent reports grounded in large scale databases. In our experiments, we find that Satyrn generates reports in which over 86% accurate claims while maintaining high levels of fluency and coherence, even when using smaller language models such as Mistral-7B, as compared to GPT-4 Code Interpreter in which just 57% of claims are accurate.

On Robustness to Adversarial Examples and Polynomial Optimization

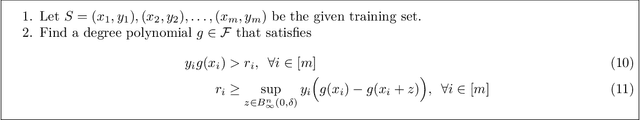
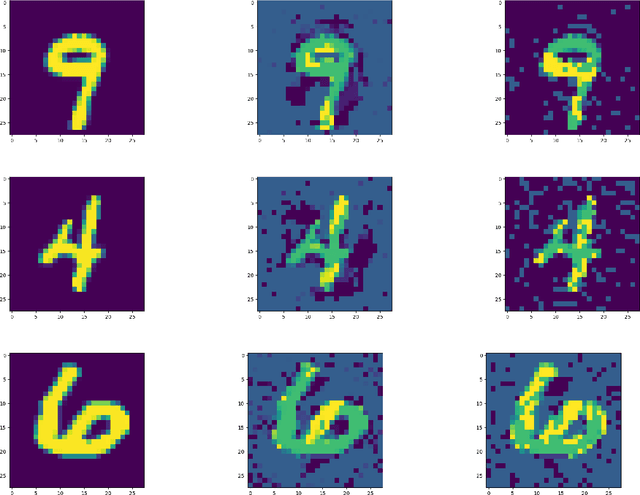
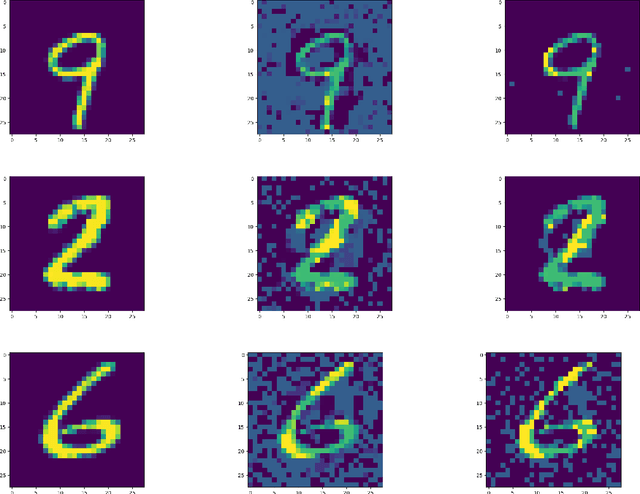
We study the design of computationally efficient algorithms with provable guarantees, that are robust to adversarial (test time) perturbations. While there has been an proliferation of recent work on this topic due to its connections to test time robustness of deep networks, there is limited theoretical understanding of several basic questions like (i) when and how can one design provably robust learning algorithms? (ii) what is the price of achieving robustness to adversarial examples in a computationally efficient manner? The main contribution of this work is to exhibit a strong connection between achieving robustness to adversarial examples, and a rich class of polynomial optimization problems, thereby making progress on the above questions. In particular, we leverage this connection to (a) design computationally efficient robust algorithms with provable guarantees for a large class of hypothesis, namely linear classifiers and degree-2 polynomial threshold functions (PTFs), (b) give a precise characterization of the price of achieving robustness in a computationally efficient manner for these classes, (c) design efficient algorithms to certify robustness and generate adversarial attacks in a principled manner for 2-layer neural networks. We empirically demonstrate the effectiveness of these attacks on real data.

Clustering Stable Instances of Euclidean k-means

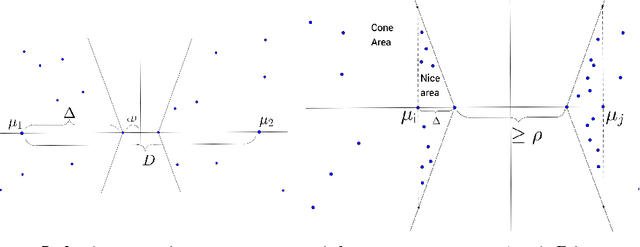
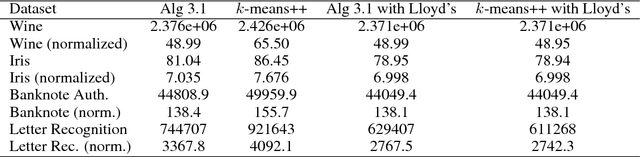
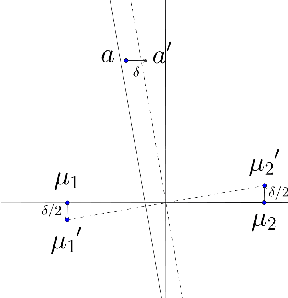
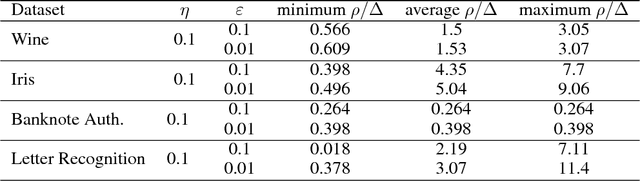
The Euclidean k-means problem is arguably the most widely-studied clustering problem in machine learning. While the k-means objective is NP-hard in the worst-case, practitioners have enjoyed remarkable success in applying heuristics like Lloyd's algorithm for this problem. To address this disconnect, we study the following question: what properties of real-world instances will enable us to design efficient algorithms and prove guarantees for finding the optimal clustering? We consider a natural notion called additive perturbation stability that we believe captures many practical instances. Stable instances have unique optimal k-means solutions that do not change even when each point is perturbed a little (in Euclidean distance). This captures the property that the k-means optimal solution should be tolerant to measurement errors and uncertainty in the points. We design efficient algorithms that provably recover the optimal clustering for instances that are additive perturbation stable. When the instance has some additional separation, we show an efficient algorithm with provable guarantees that is also robust to outliers. We complement these results by studying the amount of stability in real datasets and demonstrating that our algorithm performs well on these benchmark datasets.