On Robustness to Adversarial Examples and Polynomial Optimization
Paper and Code
Nov 12, 2019
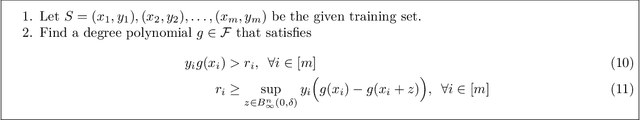
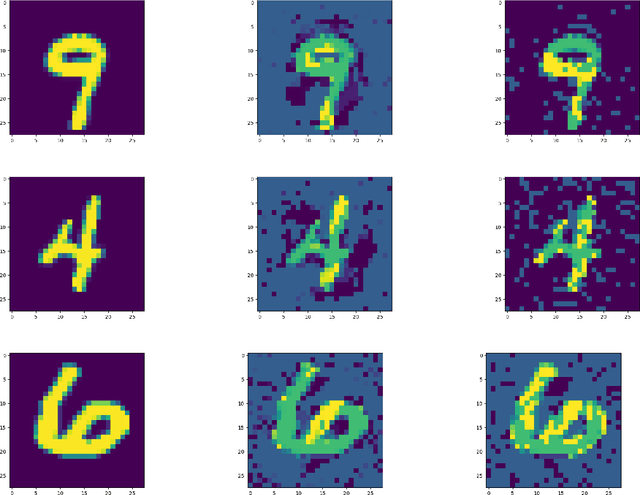
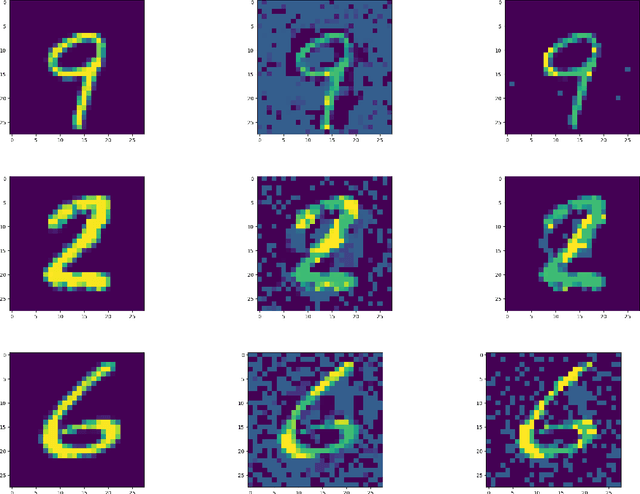
We study the design of computationally efficient algorithms with provable guarantees, that are robust to adversarial (test time) perturbations. While there has been an proliferation of recent work on this topic due to its connections to test time robustness of deep networks, there is limited theoretical understanding of several basic questions like (i) when and how can one design provably robust learning algorithms? (ii) what is the price of achieving robustness to adversarial examples in a computationally efficient manner? The main contribution of this work is to exhibit a strong connection between achieving robustness to adversarial examples, and a rich class of polynomial optimization problems, thereby making progress on the above questions. In particular, we leverage this connection to (a) design computationally efficient robust algorithms with provable guarantees for a large class of hypothesis, namely linear classifiers and degree-2 polynomial threshold functions (PTFs), (b) give a precise characterization of the price of achieving robustness in a computationally efficient manner for these classes, (c) design efficient algorithms to certify robustness and generate adversarial attacks in a principled manner for 2-layer neural networks. We empirically demonstrate the effectiveness of these attacks on real data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge