On the Query Complexity of Verifier-Assisted Language Generation

Recently, a plethora of works have proposed inference-time algorithms (e.g. best-of-n), which incorporate verifiers to assist the generation process. Their quality-efficiency trade-offs have been empirically benchmarked on a variety of constrained generation tasks, but the algorithmic design landscape is still largely poorly understood. In this paper, we develop a mathematical framework for reasoning about constrained generation using a pre-trained language model generator oracle and a process verifier--which can decide whether a prefix can be extended to a string which satisfies the constraints of choice. We show that even in very simple settings, access to a verifier can render an intractable problem (information-theoretically or computationally) to a tractable one. In fact, we show even simple algorithms, like tokenwise rejection sampling, can enjoy significant benefits from access to a verifier. Empirically, we show that a natural modification of tokenwise rejection sampling, in which the sampler is allowed to "backtrack" (i.e., erase the final few generated tokens) has robust and substantive benefits over natural baselines (e.g. (blockwise) rejection sampling, nucleus sampling)--both in terms of computational efficiency, accuracy and diversity.

Promises and Pitfalls of Generative Masked Language Modeling: Theoretical Framework and Practical Guidelines

Autoregressive language models are the currently dominant paradigm for text generation, but they have some fundamental limitations that cannot be remedied by scale-for example inherently sequential and unidirectional generation. While alternate classes of models have been explored, we have limited mathematical understanding of their fundamental power and limitations. In this paper we focus on Generative Masked Language Models (GMLMs), a non-autoregressive paradigm in which we train a model to fit conditional probabilities of the data distribution via masking, which are subsequently used as inputs to a Markov Chain to draw samples from the model, These models empirically strike a promising speed-quality trade-off as each step can be typically parallelized by decoding the entire sequence in parallel. We develop a mathematical framework for analyzing and improving such models which sheds light on questions of sample complexity and inference speed and quality. Empirically, we adapt the T5 model for iteratively-refined parallel decoding, achieving 2-3x speedup in machine translation with minimal sacrifice in quality compared with autoregressive models. We run careful ablation experiments to give recommendations on key design choices, and make fine-grained observations on the common error modes in connection with our theory. Our mathematical analyses and empirical observations characterize both potentials and limitations of this approach, and can be applied to future works on improving understanding and performance of GMLMs. Our codes are released at https://github.com/google-research/google-research/tree/master/padir

Data Cross-Segmentation for Improved Generalization in Reinforcement Learning Based Algorithmic Trading

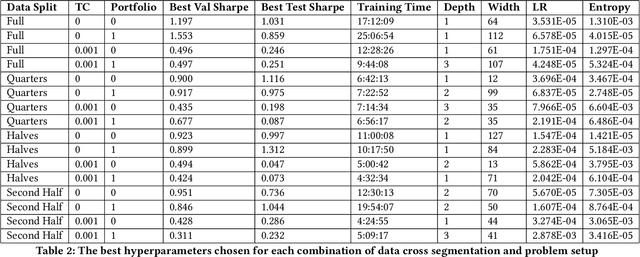
The use of machine learning in algorithmic trading systems is increasingly common. In a typical set-up, supervised learning is used to predict the future prices of assets, and those predictions drive a simple trading and execution strategy. This is quite effective when the predictions have sufficient signal, markets are liquid, and transaction costs are low. However, those conditions often do not hold in thinly traded financial markets and markets for differentiated assets such as real estate or vehicles. In these markets, the trading strategy must consider the long-term effects of taking positions that are relatively more difficult to change. In this work, we propose a Reinforcement Learning (RL) algorithm that trades based on signals from a learned predictive model and addresses these challenges. We test our algorithm on 20+ years of equity data from Bursa Malaysia.