Key-Scan-Based Mobile Robot Navigation: Integrated Mapping, Planning, and Control using Graphs of Scan Regions

Safe autonomous navigation in a priori unknown environments is an essential skill for mobile robots to reliably and adaptively perform diverse tasks (e.g., delivery, inspection, and interaction) in unstructured cluttered environments. Hybrid metric-topological maps, constructed as a pose graph of local submaps, offer a computationally efficient world representation for adaptive mapping, planning, and control at the regional level. In this paper, we consider a pose graph of locally sensed star-convex scan regions as a metric-topological map, with star convexity enabling simple yet effective local navigation strategies. We design a new family of safe local scan navigation policies and present a perception-driven feedback motion planning method through the sequential composition of local scan navigation policies, enabling provably correct and safe robot navigation over the union of local scan regions. We introduce a new concept of bridging and frontier scans for automated key scan selection and exploration for integrated mapping and navigation in unknown environments. We demonstrate the effectiveness of our key-scan-based navigation and mapping framework using a mobile robot equipped with a 360$^{\circ}$ laser range scanner in 2D cluttered environments through numerical ROS-Gazebo simulations and real hardware~experiments.

Total Turning and Motion Range Prediction for Safe Unicycle Control

Safe and smooth motion control is essential for mobile robots when performing various automation tasks around obstacles, especially in the presence of people and other mobile robots. The total turning and space used by a mobile robot while moving towards a specified goal position play a crucial role in determining the required control effort and complexity. In this paper, we consider a standard unicycle control approach based on angular feedback linearization and provide an explicit analytical measure for determining the total turning effort during unicycle control in terms of unicycle state and control gains. We show that undesired spiral oscillatory motion around the goal position can be avoided by choosing a higher angular control gain compared to the linear control gain. Accordingly, we establish an accurate, explicit triangular motion range bound on the closed-loop unicycle trajectory using the total turning effort. The improved accuracy in motion range prediction results from a stronger dependency on the unicycle state and control parameters. To compare alternative circular, conic, and triangular motion range prediction approaches, we present an application of the proposed unicycle motion control and motion prediction methods for safe unicycle path following around obstacles in numerical simulations.

Graph-Theoretic Bézier Curve Optimization over Safe Corridors for Safe and Smooth Motion Planning

As a parametric motion representation, B\'ezier curves have significant applications in polynomial trajectory optimization for safe and smooth motion planning of various robotic systems, including flying drones, autonomous vehicles, and robotic manipulators. An essential component of B\'ezier curve optimization is the optimization objective, as it significantly influences the resulting robot motion. Standard physical optimization objectives, such as minimizing total velocity, acceleration, jerk, and snap, are known to yield quadratic optimization of B\'ezier curve control points. In this paper, we present a unifying graph-theoretic perspective for defining and understanding B\'ezier curve optimization objectives using a consensus distance of B\'ezier control points derived based on their interaction graph Laplacian. In addition to demonstrating how standard physical optimization objectives define a consensus distance between B\'ezier control points, we also introduce geometric and statistical optimization objectives as alternative consensus distances, constructed using finite differencing and differential variance. To compare these optimization objectives, we apply B\'ezier curve optimization over convex polygonal safe corridors that are automatically constructed around a maximal-clearance minimal-length reference path. We provide an explicit analytical formulation for quadratic optimization of B\'ezier curves using B\'ezier matrix operations. We conclude that the norm and variance of the finite differences of B\'ezier control points lead to simpler and more intuitive interaction graphs and optimization objectives compared to B\'ezier derivative norms, despite having similar robot motion profiles.

Adaptive Headway Motion Control and Motion Prediction for Safe Unicycle Motion Design

Differential drive robots that can be modeled as a kinematic unicycle are a standard mobile base platform for many service and logistics robots. Safe and smooth autonomous motion around obstacles is a crucial skill for unicycle robots to perform diverse tasks in complex environments. A classical control approach for unicycle control is feedback linearization using a headway point at a fixed headway distance in front of the unicycle. The unicycle headway control brings the headway point to a desired goal location by embedding a linear headway reference dynamics, which often results in an undesired offset for the actual unicycle position. In this paper, we introduce a new unicycle headway control approach with an adaptive headway distance that overcomes this limitation, i.e., when the headway point reaches the goal the unicycle position is also at the goal. By systematically analyzing the closed-loop unicycle motion under the adaptive headway controller, we design analytical feedback motion prediction methods that bound the closed-loop unicycle position trajectory and so can be effectively used for safety assessment and safe unicycle motion design around obstacles. We present an application of adaptive headway motion control and motion prediction for safe unicycle path following around obstacles in numerical simulations.

Time Governors for Safe Path-Following Control

Safe and smooth robot motion around obstacles is an essential skill for autonomous robots, especially when operating around people and other robots. Conventionally, due to real-time operation requirements and onboard computation limitations, many robot motion planning and control methods follow a two-step approach: first construct a (e.g., piecewise linear) collision-free reference path for a simplified robot model, and then execute the reference plan via path-following control for a more accurate and complex robot model. A challenge of such a decoupled robot motion planning and control method for highly dynamic robotic systems is ensuring the safety of path-following control as well as the successful completion of the reference plan. In this paper, we introduce a novel dynamical systems approach for online closed-loop time parametrization, called $\textit{a time governor}$, of a reference path for provably correct and safe path-following control based on feedback motion prediction, where the safety of robot motion under path-following control is continuously monitored using predicted robot motion. After introducing the general framework of time governors for safe path following, we present an example application for the fully actuated high-order robot dynamics using proportional-and-higher-order-derivative (PhD) path-following control whose feedback motion prediction is performed by Lyapunov ellipsoids and Vandemonde simplexes. In numerical simulations, we investigate the role of reference position and velocity feedback, and motion prediction on path-following performance and robot motion.

Feedback Motion Prediction for Safe Unicycle Robot Navigation

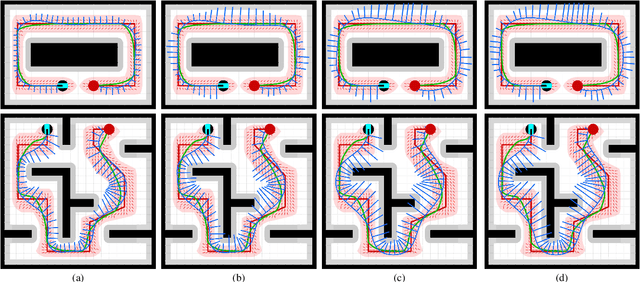
As a simple and robust mobile robot base, differential drive robots that can be modelled as a kinematic unicycle find significant applications in logistics and service robotics in both industrial and domestic settings. Safe robot navigation around obstacles is an essential skill for such unicycle robots to perform diverse useful tasks in complex cluttered environments, especially around people and other robots. In this paper, as a more accurate alternative to the standard circular Lyapunov level sets, we introduce novel conic feedback motion prediction methods for bounding the close-loop motion trajectory of the kinematic unicycle robot model under a standard unicycle motion control approach. We present an application of unicycle feedback motion prediction for safe robot navigation using a reference governor, where the safety of the unicycle motion is continuously monitored based on the predicted robot motion. We investigate the role of motion prediction on robot behaviour in numerical simulations and conclude that accurate feedback motion prediction is key for safe and fast robot navigation.

From Low to High Order Motion Planners: Safe Robot Navigation using Motion Prediction and Reference Governor

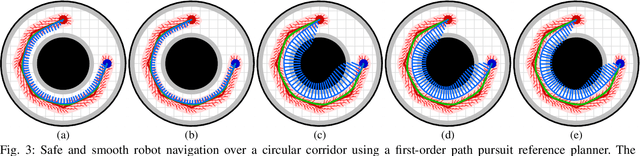
Safe navigation around obstacles is a fundamental challenge for highly dynamic robots. The state-of-the-art approach for adapting simple reference path planners to complex robot dynamics using trajectory optimization and tracking control is brittle and requires significant replanning cycles. In this paper, we introduce a novel feedback motion planning framework that extends the applicability of low-order (e.g. position-/velocity-controlled) reference motion planners to high-order (e.g., acceleration-/jerk-controlled) robot models using motion prediction and reference governors. We use predicted robot motion range for safety assessment and establish a bidirectional interface between high-level planning and low-level control via a reference governor. We describe the generic fundamental building blocks of our feedback motion planning framework and give specific example constructions for motion control, prediction, and reference planning. We prove the correctness of our planning framework and demonstrate its performance in numerical simulations. We conclude that accurate motion prediction is crucial for closing the gap between high-level planning and low-level control.

Adaptive Bézier Degree Reduction and Splitting for Computationally Efficient Motion Planning

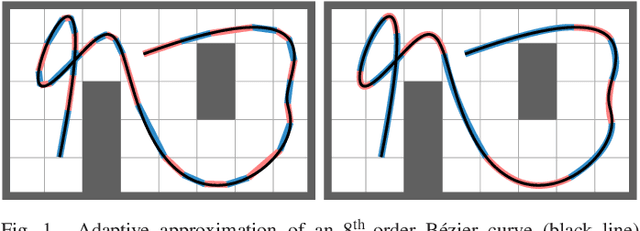
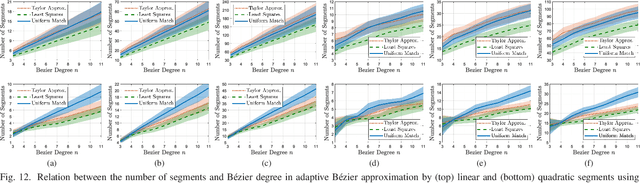
As a parametric polynomial curve family, B\'ezier curves are widely used in safe and smooth motion design of intelligent robotic systems from flying drones to autonomous vehicles to robotic manipulators. In such motion planning settings, the critical features of high-order B\'ezier curves such as curve length, distance-to-collision, maximum curvature/velocity/acceleration are either numerically computed at a high computational cost or inexactly approximated by discrete samples. To address these issues, in this paper we present a novel computationally efficient approach for adaptive approximation of high-order B\'ezier curves by multiple low-order B\'ezier segments at any desired level of accuracy that is specified in terms of a B\'ezier metric. Accordingly, we introduce a new B\'ezier degree reduction method, called parameterwise matching reduction, that approximates B\'ezier curves more accurately compared to the standard least squares and Taylor reduction methods. We also propose a new B\'ezier metric, called the maximum control-point distance, that can be computed analytically, has a strong equivalence relation with other existing B\'ezier metrics, and defines a geometric relative bound between B\'ezier curves. We provide extensive numerical evidence to demonstrate the effectiveness of our proposed B\'ezier approximation approach. As a rule of thumb, based on the degree-one matching reduction error, we conclude that an $n^\text{th}$-order B\'ezier curve can be accurately approximated by $3(n-1)$ quadratic and $6(n-1)$ linear B\'ezier segments, which is fundamental for B\'ezier discretization.