Aron Tiemessen
Adaptive Bézier Degree Reduction and Splitting for Computationally Efficient Motion Planning
Jan 19, 2022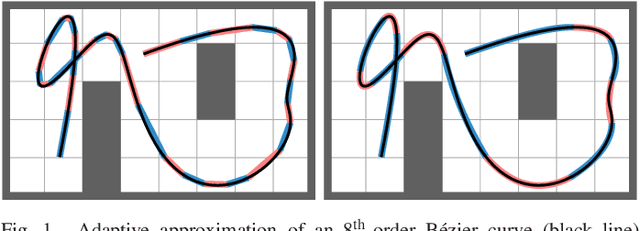


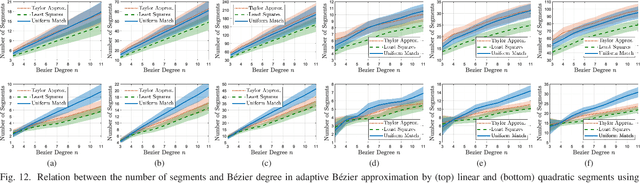
Abstract:As a parametric polynomial curve family, B\'ezier curves are widely used in safe and smooth motion design of intelligent robotic systems from flying drones to autonomous vehicles to robotic manipulators. In such motion planning settings, the critical features of high-order B\'ezier curves such as curve length, distance-to-collision, maximum curvature/velocity/acceleration are either numerically computed at a high computational cost or inexactly approximated by discrete samples. To address these issues, in this paper we present a novel computationally efficient approach for adaptive approximation of high-order B\'ezier curves by multiple low-order B\'ezier segments at any desired level of accuracy that is specified in terms of a B\'ezier metric. Accordingly, we introduce a new B\'ezier degree reduction method, called parameterwise matching reduction, that approximates B\'ezier curves more accurately compared to the standard least squares and Taylor reduction methods. We also propose a new B\'ezier metric, called the maximum control-point distance, that can be computed analytically, has a strong equivalence relation with other existing B\'ezier metrics, and defines a geometric relative bound between B\'ezier curves. We provide extensive numerical evidence to demonstrate the effectiveness of our proposed B\'ezier approximation approach. As a rule of thumb, based on the degree-one matching reduction error, we conclude that an $n^\text{th}$-order B\'ezier curve can be accurately approximated by $3(n-1)$ quadratic and $6(n-1)$ linear B\'ezier segments, which is fundamental for B\'ezier discretization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge