Wide Graph Neural Networks: Aggregation Provably Leads to Exponentially Trainability Loss
Paper and Code
Mar 03, 2021
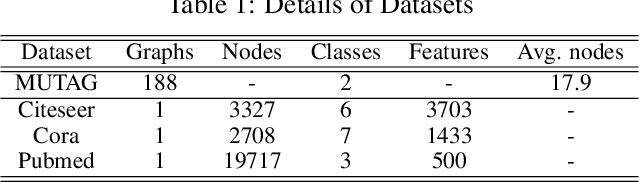


Graph convolutional networks (GCNs) and their variants have achieved great success in dealing with graph-structured data. However, it is well known that deep GCNs will suffer from over-smoothing problem, where node representations tend to be indistinguishable as we stack up more layers. Although extensive research has confirmed this prevailing understanding, few theoretical analyses have been conducted to study the expressivity and trainability of deep GCNs. In this work, we demonstrate these characterizations by studying the Gaussian Process Kernel (GPK) and Graph Neural Tangent Kernel (GNTK) of an infinitely-wide GCN, corresponding to the analysis on expressivity and trainability, respectively. We first prove the expressivity of infinitely-wide GCNs decaying at an exponential rate by applying the mean-field theory on GPK. Besides, we formulate the asymptotic behaviors of GNTK in the large depth, which enables us to reveal the dropping trainability of wide and deep GCNs at an exponential rate. Additionally, we extend our theoretical framework to analyze residual connection-resemble techniques. We found that these techniques can mildly mitigate exponential decay, but they failed to overcome it fundamentally. Finally, all theoretical results in this work are corroborated experimentally on a variety of graph-structured datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge