Verifying Probabilistic Specifications with Functional Lagrangians

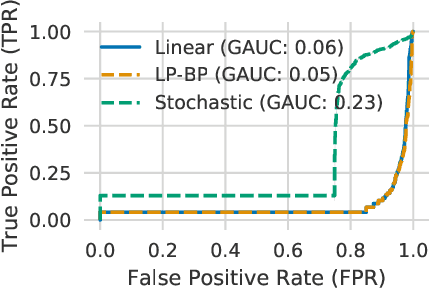
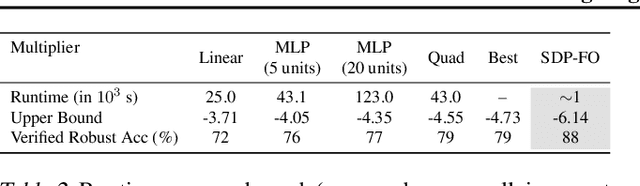
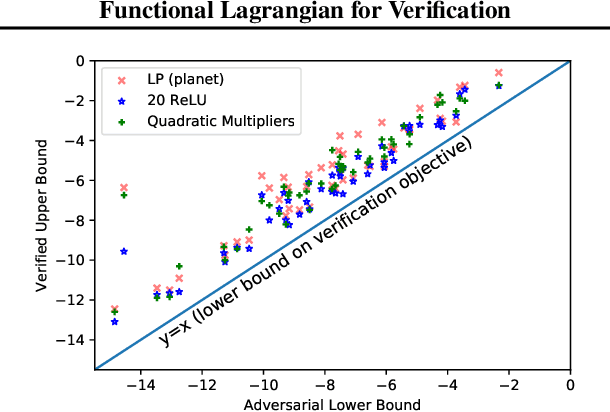
We propose a general framework for verifying input-output specifications of neural networks using functional Lagrange multipliers that generalizes standard Lagrangian duality. We derive theoretical properties of the framework, which can handle arbitrary probabilistic specifications, showing that it provably leads to tight verification when a sufficiently flexible class of functional multipliers is chosen. With a judicious choice of the class of functional multipliers, the framework can accommodate desired trade-offs between tightness and complexity. We demonstrate empirically that the framework can handle a diverse set of networks, including Bayesian neural networks with Gaussian posterior approximations, MC-dropout networks, and verify specifications on adversarial robustness and out-of-distribution(OOD) detection. Our framework improves upon prior work in some settings and also generalizes to new stochastic networks and probabilistic specifications, like distributionally robust OOD detection.