Using Program Synthesis and Inductive Logic Programming to solve Bongard Problems
Paper and Code
Oct 19, 2021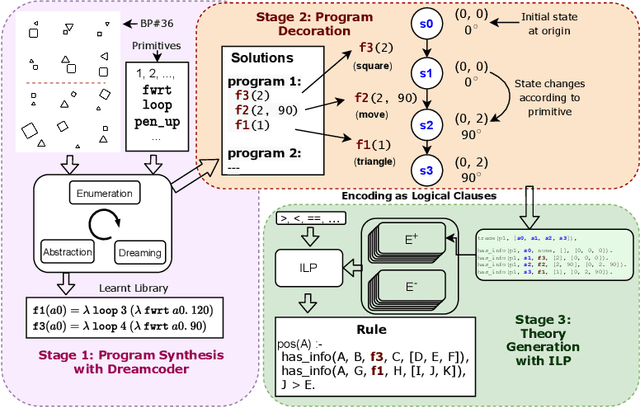

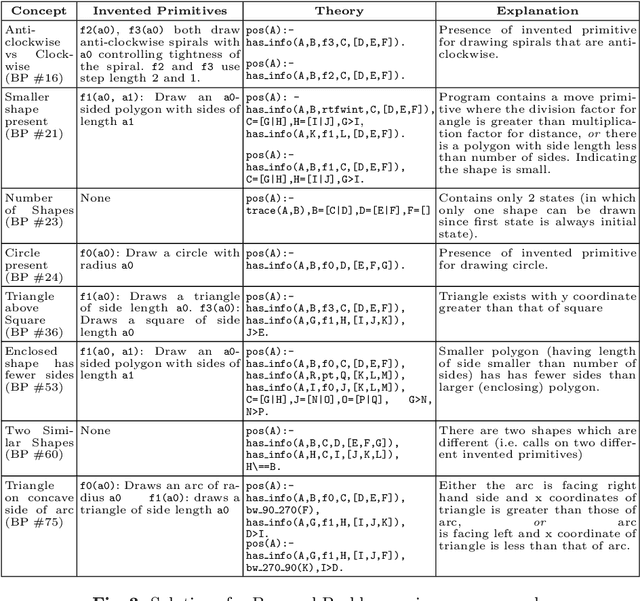
The ability to recognise and make analogies is often used as a measure or test of human intelligence. The ability to solve Bongard problems is an example of such a test. It has also been postulated that the ability to rapidly construct novel abstractions is critical to being able to solve analogical problems. Given an image, the ability to construct a program that would generate that image is one form of abstraction, as exemplified in the Dreamcoder project. In this paper, we present a preliminary examination of whether programs constructed by Dreamcoder can be used for analogical reasoning to solve certain Bongard problems. We use Dreamcoder to discover programs that generate the images in a Bongard problem and represent each of these as a sequence of state transitions. We decorate the states using positional information in an automated manner and then encode the resulting sequence into logical facts in Prolog. We use inductive logic programming (ILP), to learn an (interpretable) theory for the abstract concept involved in an instance of a Bongard problem. Experiments on synthetically created Bongard problems for concepts such as 'above/below' and 'clockwise/counterclockwise' demonstrate that our end-to-end system can solve such problems. We study the importance and completeness of each component of our approach, highlighting its current limitations and pointing to directions for improvement in our formulation as well as in elements of any Dreamcoder-like program synthesis system used for such an approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge