Unsupervised diffeomorphic cardiac image registration using parameterization of the deformation field
Paper and Code
Aug 28, 2022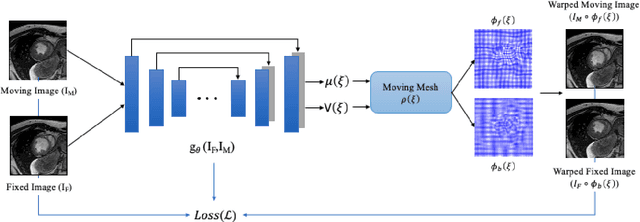

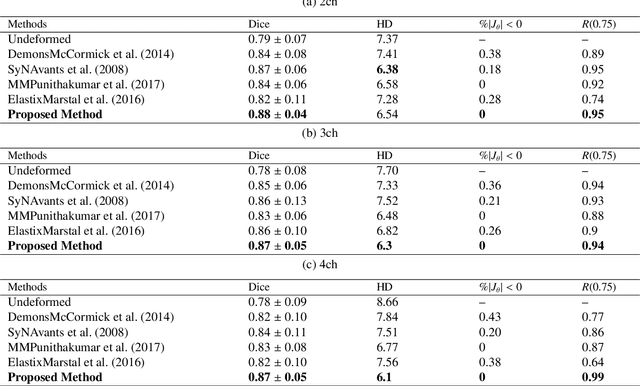

This study proposes an end-to-end unsupervised diffeomorphic deformable registration framework based on moving mesh parameterization. Using this parameterization, a deformation field can be modeled with its transformation Jacobian determinant and curl of end velocity field. The new model of the deformation field has three important advantages; firstly, it relaxes the need for an explicit regularization term and the corresponding weight in the cost function. The smoothness is implicitly embedded in the solution which results in a physically plausible deformation field. Secondly, it guarantees diffeomorphism through explicit constraints applied to the transformation Jacobian determinant to keep it positive. Finally, it is suitable for cardiac data processing, since the nature of this parameterization is to define the deformation field in terms of the radial and rotational components. The effectiveness of the algorithm is investigated by evaluating the proposed method on three different data sets including 2D and 3D cardiac MRI scans. The results demonstrate that the proposed framework outperforms existing learning-based and non-learning-based methods while generating diffeomorphic transformations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge