Tree Search Techniques for Minimizing Detectability and Maximizing Visibility
Paper and Code
Feb 22, 2019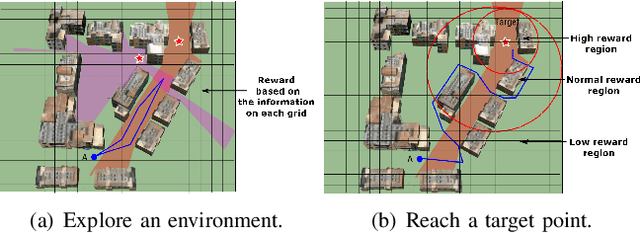
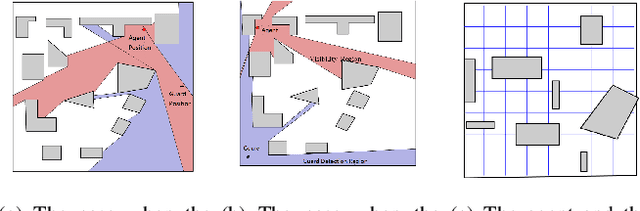
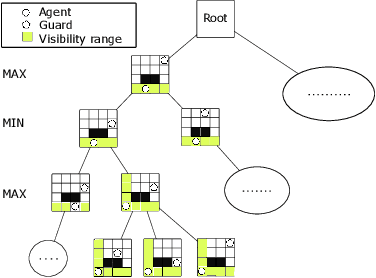
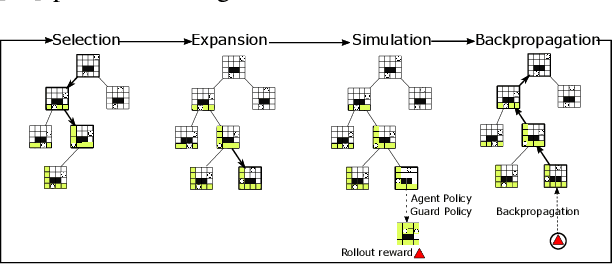
We introduce and study the problem of planning a trajectory for an agent to carry out a scouting mission while avoiding being detected by an adversarial guard. This introduces an adversarial version of classical visibility-based planning problems such as the Watchman Route Problem. The agent receives a positive reward for increasing its visibility and a negative penalty when it is detected by the guard. The objective is to find a finite-horizon path for the agent that balances the trade-off maximizing visibility and minimizing detectability. We model this problem as a sequential two-player zero-sum discrete game. A minimax tree search can give the optimal policy for the agent but requires an exponential-time computation and space. We propose several pruning techniques to reduce the computational cost while still preserving optimality guarantees. Simulation results show that the proposed strategy prunes approximately three orders of magnitude nodes as compared to the brute-force strategy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge