Towards Discovering Neural Architectures from Scratch

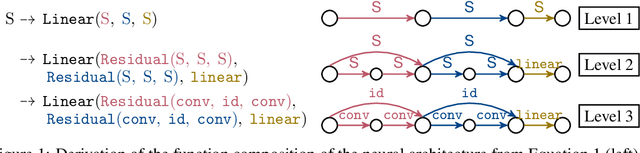
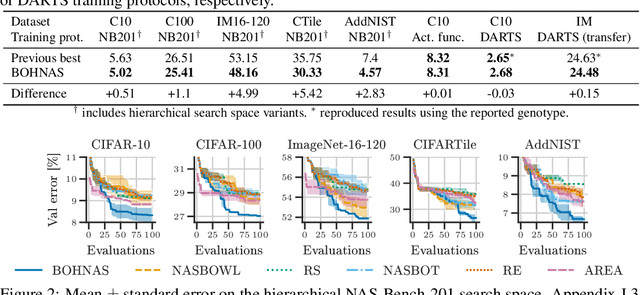
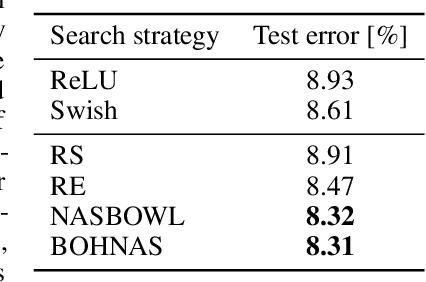
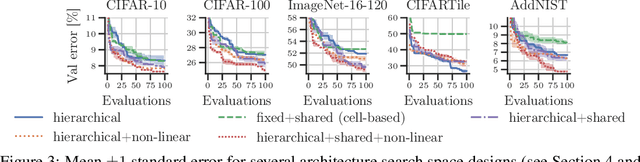
The discovery of neural architectures from scratch is the long-standing goal of Neural Architecture Search (NAS). Searching over a wide spectrum of neural architectures can facilitate the discovery of previously unconsidered but well-performing architectures. In this work, we take a large step towards discovering neural architectures from scratch by expressing architectures algebraically. This algebraic view leads to a more general method for designing search spaces, which allows us to compactly represent search spaces that are 100s of orders of magnitude larger than common spaces from the literature. Further, we propose a Bayesian Optimization strategy to efficiently search over such huge spaces, and demonstrate empirically that both our search space design and our search strategy can be superior to existing baselines. We open source our algebraic NAS approach and provide APIs for PyTorch and TensorFlow.