The hidden label-marginal biases of segmentation losses
Paper and Code
Apr 18, 2021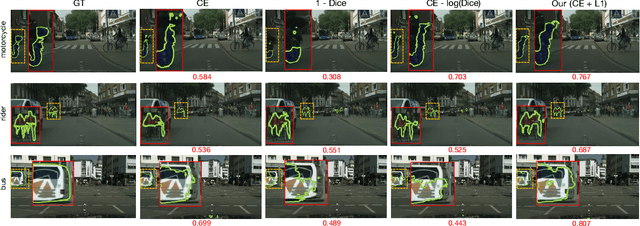
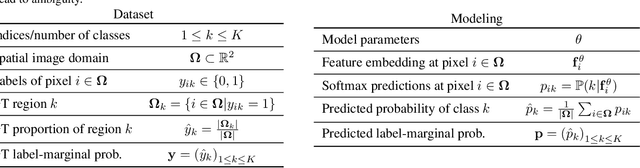
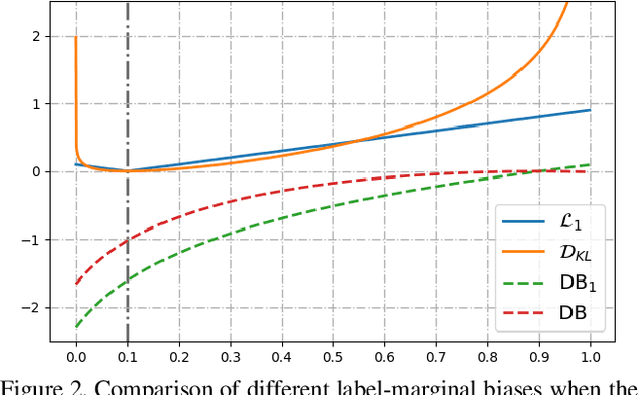
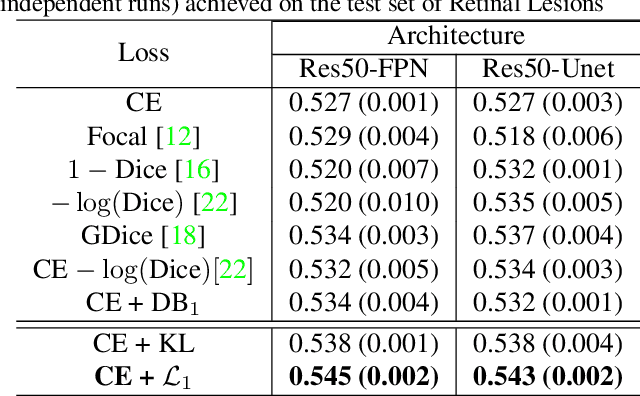
Most segmentation losses are arguably variants of the Cross-Entropy (CE) or Dice loss. In the literature, there is no clear consensus as to which of these losses is a better choice, with varying performances for each across different benchmarks and applications. We develop a theoretical analysis that links these two types of losses, exposing their advantages and weaknesses. First, we explicitly demonstrate that CE and Dice share a much deeper connection than previously thought: CE is an upper bound on both logarithmic and linear Dice losses. Furthermore, we provide an information-theoretic analysis, which highlights hidden label-marginal biases : Dice has an intrinsic bias towards imbalanced solutions, whereas CE implicitly encourages the ground-truth region proportions. Our theoretical results explain the wide experimental evidence in the medical-imaging literature, whereby Dice losses bring improvements for imbalanced segmentation. It also explains why CE dominates natural-image problems with diverse class proportions, in which case Dice might have difficulty adapting to different label-marginal distributions. Based on our theoretical analysis, we propose a principled and simple solution, which enables to control explicitly the label-marginal bias. Our loss integrates CE with explicit ${\cal L}_1$ regularization, which encourages label marginals to match target class proportions, thereby mitigating class imbalance but without losing generality. Comprehensive experiments and ablation studies over different losses and applications validate our theoretical analysis, as well as the effectiveness of our explicit label-marginal regularizers.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge