$t$-$k$-means: A $k$-means Variant with Robustness and Stability

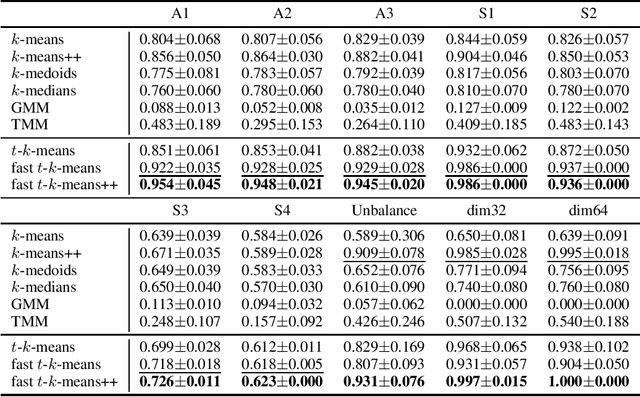
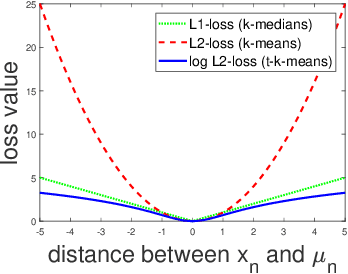
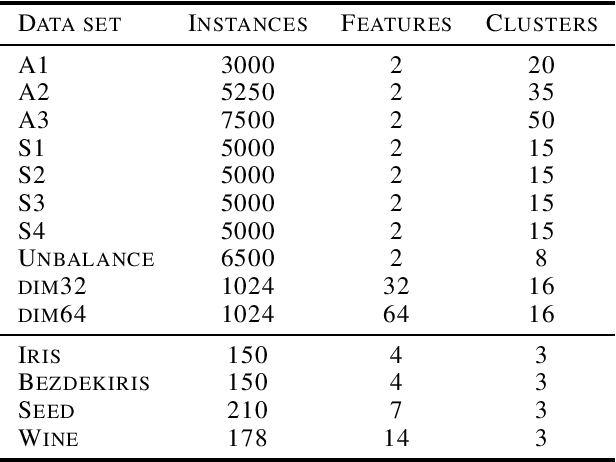
Lloyd's $k$-means algorithm is one of the most classical clustering method, which is widely used in data mining or as a data pre-processing procedure. However, due to the thin-tailed property of the Gaussian distribution, $k$-means suffers from relatively poor performance on the heavy-tailed data or outliers. In addition, $k$-means have a relatively weak stability, $i.e.$ its result has a large variance, which reduces the credibility of the model. In this paper, we propose a robust and stable $k$-means variant, the $t$-$k$-means, as well as its fast version in solving the flat clustering problem. Theoretically, we detail the derivations of $t$-$k$-means and analyze its robustness and stability from the aspect of loss function, influence function and the expression of clustering center. A large number of experiments are conducted, which empirically demonstrates that our method has empirical soundness while preserving running efficiency.