Super-Resolution Harmonic Retrieval of Non-Circular Signals
Paper and Code
Jan 17, 2023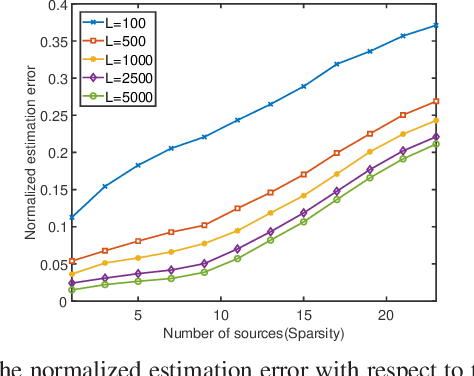

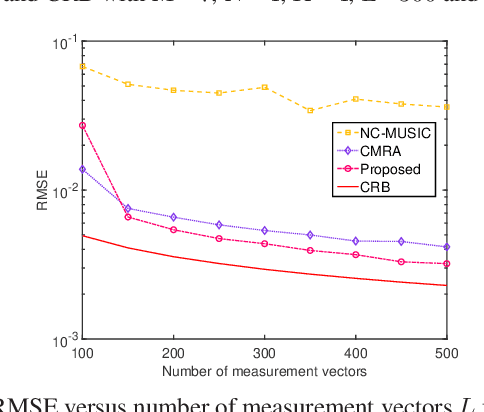
This paper proposes a super-resolution harmonic retrieval method for uncorrelated strictly non-circular signals, whose covariance and pseudo-covariance present Toeplitz and Hankel structures, respectively. Accordingly, the augmented covariance matrix constructed by the covariance and pseudo-covariance matrices is not only low rank but also jointly Toeplitz-Hankel structured. To efficiently exploit such a desired structure for high estimation accuracy, we develop a low-rank Toeplitz-Hankel covariance reconstruction (LRTHCR) solution employed over the augmented covariance matrix. Further, we design a fitting error constraint to flexibly implement the LRTHCR algorithm without knowing the noise statistics. In addition, performance analysis is provided for the proposed LRTHCR in practical settings. Simulation results reveal that the LRTHCR outperforms the benchmark methods in terms of lower estimation errors.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge