Subgraph Networks with Application to Structural Feature Space Expansion

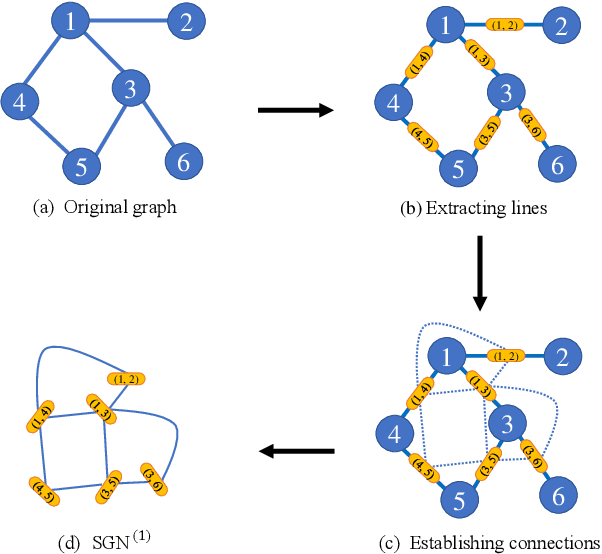
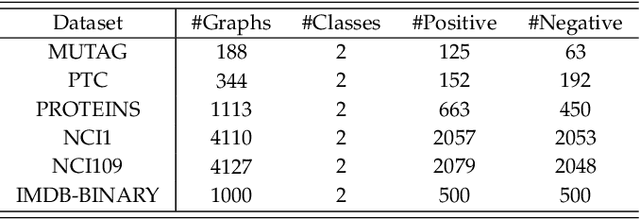
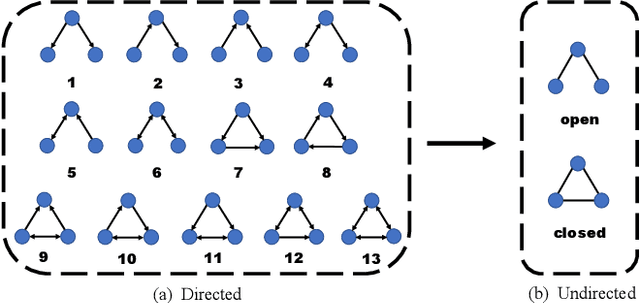
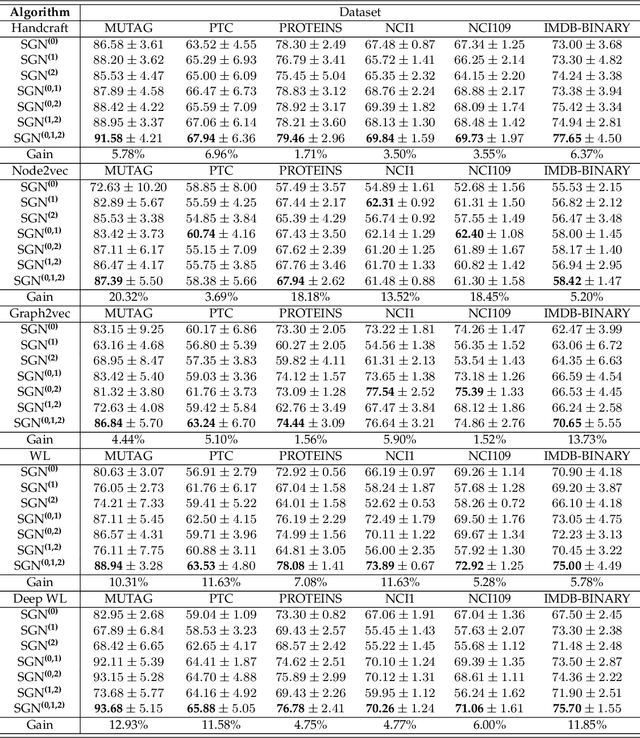
In this paper, the concept of subgraph network (SGN) is introduced and then applied to network models, with algorithms designed for constructing the 1st-order and 2nd-order SGNs, which can be easily extended to build higher-order ones. Furthermore, these SGNs are used to expand the structural feature space of the underlying network, beneficial for network classification. Numerical experiments demonstrate that the network classification model based on the structural features of the original network together with the 1st-order and 2nd-order SGNs always performs the best as compared to the models based only on one or two of such networks. In other words, the structural features of SGNs can complement that of the original network for better network classification, regardless of the feature extraction method used, such as the handcrafted, network embedding and kernel-based methods. More interestingly, it is found that the model based on the handcrafted feature performs even better than those based on automatically generated features, at least for most datasets tested in the present investigation. This indicates that, in general, properly chosen structural features are not only more interpretable due to their clear physical meanings, but also effective in designing structure-based algorithms for network classification.