Stochastic Behavior of the Nonnegative Least Mean Fourth Algorithm for Stationary Gaussian Inputs and Slow Learning
Paper and Code
Aug 24, 2015
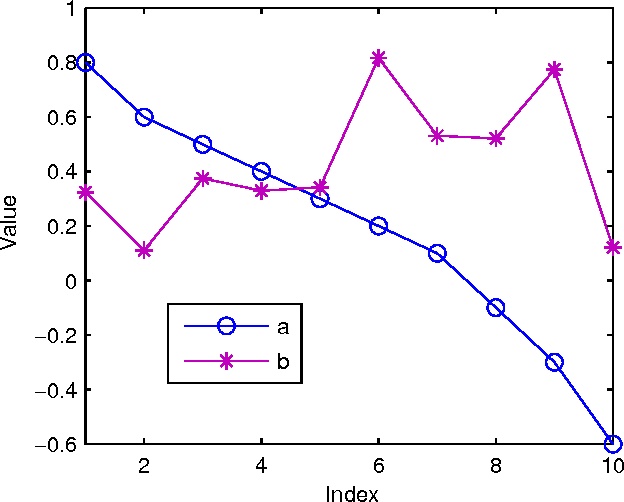
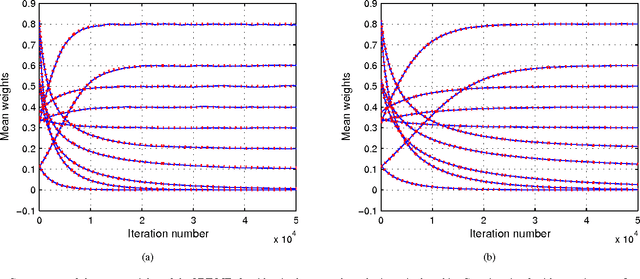

Some system identification problems impose nonnegativity constraints on the parameters to estimate due to inherent physical characteristics of the unknown system. The nonnegative least-mean-square (NNLMS) algorithm and its variants allow to address this problem in an online manner. A nonnegative least mean fourth (NNLMF) algorithm has been recently proposed to improve the performance of these algorithms in cases where the measurement noise is not Gaussian. This paper provides a first theoretical analysis of the stochastic behavior of the NNLMF algorithm for stationary Gaussian inputs and slow learning. Simulation results illustrate the accuracy of the proposed analysis.
* 11 pages, 8 figures, submitted for publication
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge