Stable Prediction on Graphs with Agnostic Distribution Shift
Paper and Code
Oct 08, 2021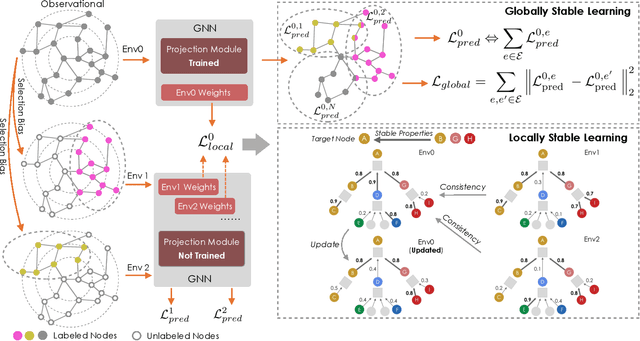
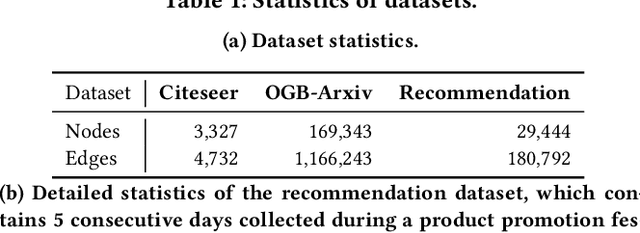
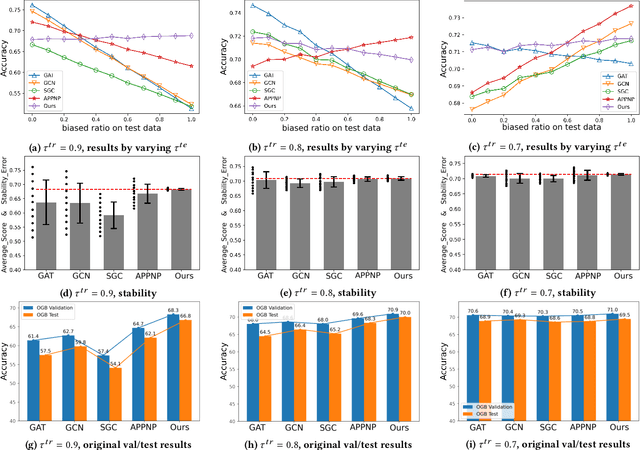
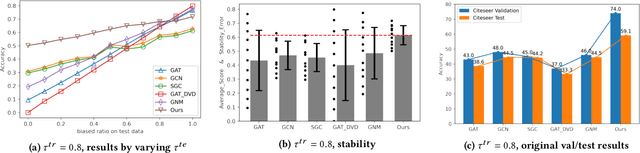
Graph is a flexible and effective tool to represent complex structures in practice and graph neural networks (GNNs) have been shown to be effective on various graph tasks with randomly separated training and testing data. In real applications, however, the distribution of training graph might be different from that of the test one (e.g., users' interactions on the user-item training graph and their actual preference on items, i.e., testing environment, are known to have inconsistencies in recommender systems). Moreover, the distribution of test data is always agnostic when GNNs are trained. Hence, we are facing the agnostic distribution shift between training and testing on graph learning, which would lead to unstable inference of traditional GNNs across different test environments. To address this problem, we propose a novel stable prediction framework for GNNs, which permits both locally and globally stable learning and prediction on graphs. In particular, since each node is partially represented by its neighbors in GNNs, we propose to capture the stable properties for each node (locally stable) by re-weighting the information propagation/aggregation processes. For global stability, we propose a stable regularizer that reduces the training losses on heterogeneous environments and thus warping the GNNs to generalize well. We conduct extensive experiments on several graph benchmarks and a noisy industrial recommendation dataset that is collected from 5 consecutive days during a product promotion festival. The results demonstrate that our method outperforms various SOTA GNNs for stable prediction on graphs with agnostic distribution shift, including shift caused by node labels and attributes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge