Spectral Unmixing via Data-guided Sparsity
Paper and Code
Nov 17, 2014
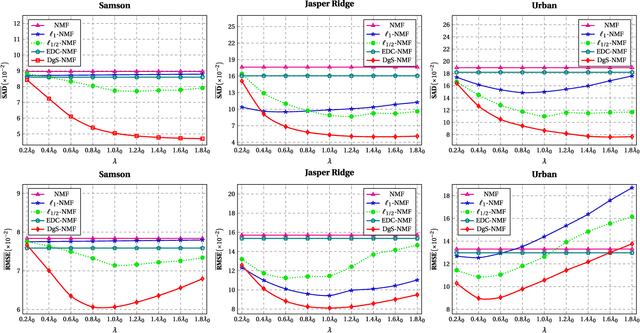
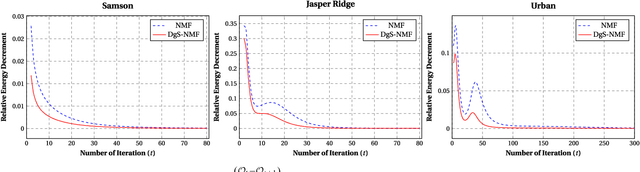
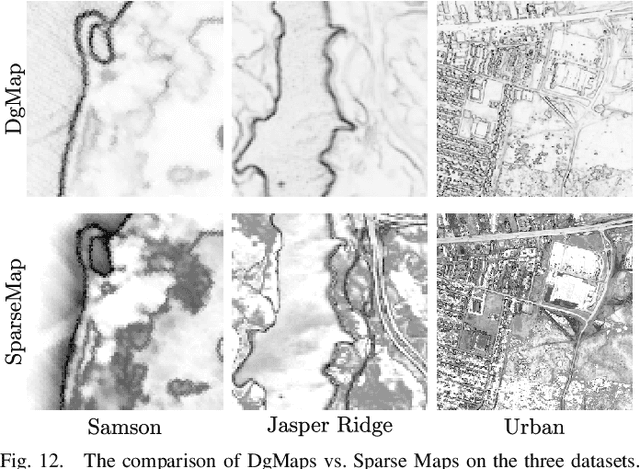
Hyperspectral unmixing, the process of estimating a common set of spectral bases and their corresponding composite percentages at each pixel, is an important task for hyperspectral analysis, visualization and understanding. From an unsupervised learning perspective, this problem is very challenging---both the spectral bases and their composite percentages are unknown, making the solution space too large. To reduce the solution space, many approaches have been proposed by exploiting various priors. In practice, these priors would easily lead to some unsuitable solution. This is because they are achieved by applying an identical strength of constraints to all the factors, which does not hold in practice. To overcome this limitation, we propose a novel sparsity based method by learning a data-guided map to describe the individual mixed level of each pixel. Through this data-guided map, the $\ell_{p}(0<p<1)$ constraint is applied in an adaptive manner. Such implementation not only meets the practical situation, but also guides the spectral bases toward the pixels under highly sparse constraint. What's more, an elegant optimization scheme as well as its convergence proof have been provided in this paper. Extensive experiments on several datasets also demonstrate that the data-guided map is feasible, and high quality unmixing results could be obtained by our method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge