Solving Math Word Problems by Scoring Equations with Recursive Neural Networks

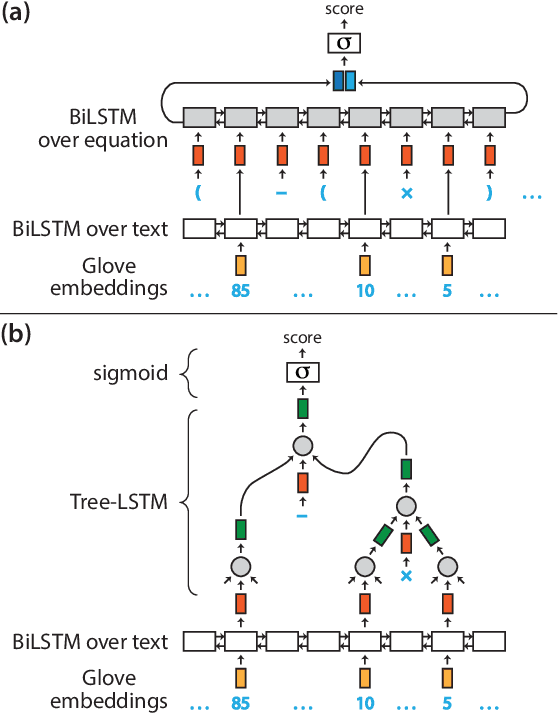
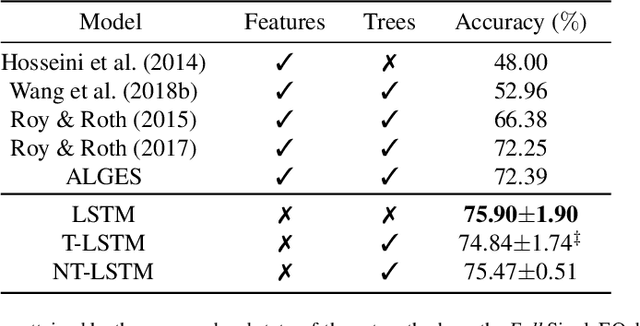
Solving math word problems is a cornerstone task in assessing language understanding and reasoning capabilities in NLP systems. Recent works use automatic extraction and ranking of candidate solution equations providing the answer to math word problems. In this work, we explore novel approaches to score such candidate solution equations using tree-structured recursive neural network (Tree-RNN) configurations. The advantage of this Tree-RNN approach over using more established sequential representations, is that it can naturally capture the structure of the equations. Our proposed method consists in transforming the mathematical expression of the equation into an expression tree. Further, we encode this tree into a Tree-RNN by using different Tree-LSTM architectures. Experimental results show that our proposed method (i) improves overall performance with more than 3% accuracy points compared to previous state-of-the-art, and with over 18% points on a subset of problems that require more complex reasoning, and (ii) outperforms sequential LSTMs by 4% accuracy points on such more complex problems.