SmoothGNN: Smoothing-based GNN for Unsupervised Node Anomaly Detection
Paper and Code
May 27, 2024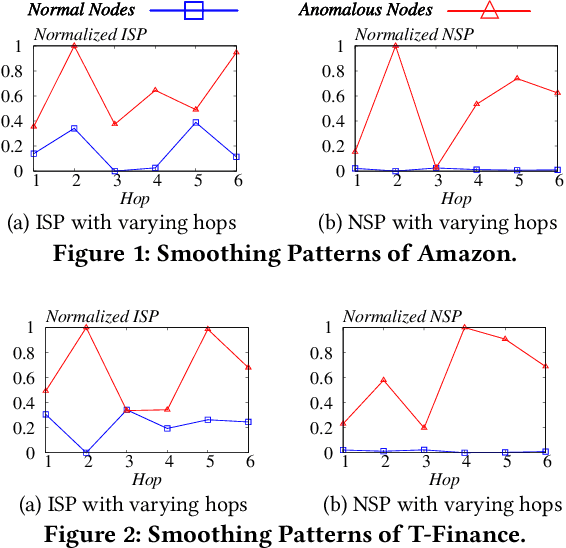
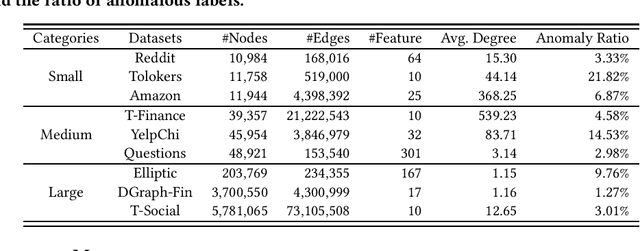
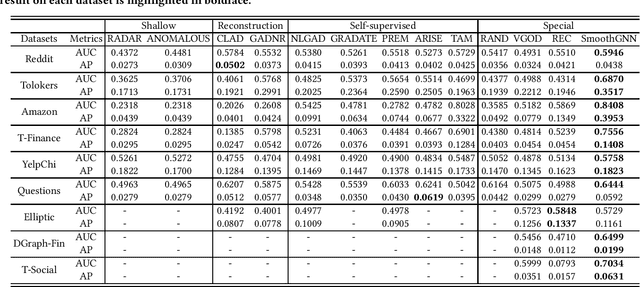
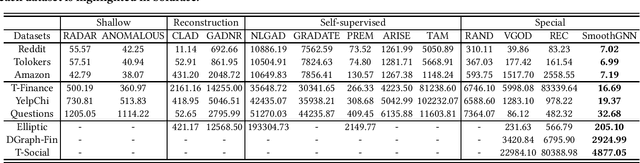
The smoothing issue leads to indistinguishable node representations, which poses a significant challenge in the field of graph learning. However, this issue also presents an opportunity to reveal underlying properties behind different types of nodes, which have been overlooked in previous studies. Through empirical and theoretical analysis of real-world node anomaly detection (NAD) datasets, we observe that anomalous and normal nodes show different patterns in the smoothing process, which can be leveraged to enhance NAD tasks. Motivated by these findings, in this paper, we propose a novel unsupervised NAD framework. Specifically, according to our theoretical analysis, we design a Smoothing Learning Component. Subsequently, we introduce a Smoothing-aware Spectral Graph Neural Network, which establishes the connection between the spectral space of graphs and the smoothing process. Additionally, we demonstrate that the Dirichlet Energy, which reflects the smoothness of a graph, can serve as coefficients for node representations across different dimensions of the spectral space. Building upon these observations and analyses, we devise a novel anomaly measure for the NAD task. Extensive experiments on 9 real-world datasets show that SmoothGNN outperforms the best rival by an average of 14.66% in AUC and 7.28% in Precision, with 75x running time speed-up, which validates the effectiveness and efficiency of our framework.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge