Self-Organized Polynomial-Time Coordination Graphs

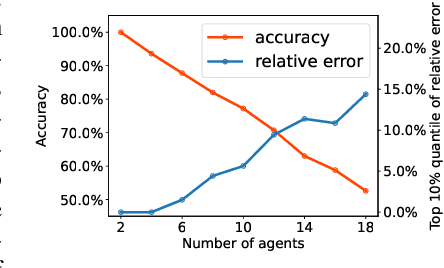
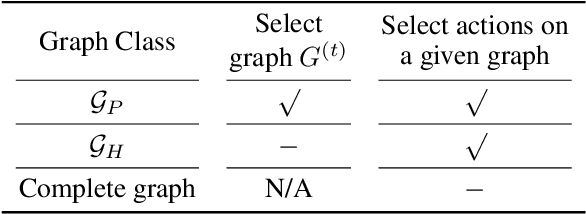
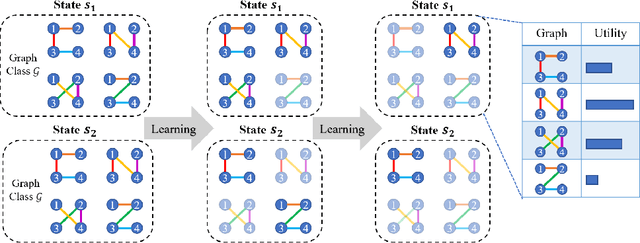
Coordination graph is a promising approach to model agent collaboration in multi-agent reinforcement learning. It factorizes a large multi-agent system into a suite of overlapping groups that represent the underlying coordination dependencies. One critical challenge in this paradigm is the complexity of computing maximum-value actions for a graph-based value factorization. It refers to the decentralized constraint optimization problem (DCOP), which and whose constant-ratio approximation are NP-hard problems. To bypass this fundamental hardness, this paper proposes a novel method, named Self-Organized Polynomial-time Coordination Graphs (SOP-CG), which uses structured graph classes to guarantee the optimality of the induced DCOPs with sufficient function expressiveness. We extend the graph topology to be state-dependent, formulate the graph selection as an imaginary agent, and finally derive an end-to-end learning paradigm from the unified Bellman optimality equation. In experiments, we show that our approach learns interpretable graph topologies, induces effective coordination, and improves performance across a variety of cooperative multi-agent tasks.