Self-learn to Explain Siamese Networks Robustly
Paper and Code
Sep 15, 2021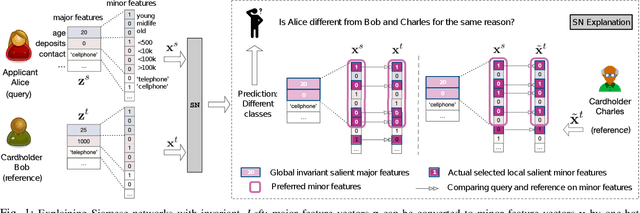
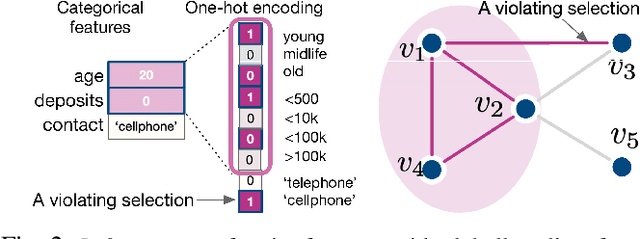
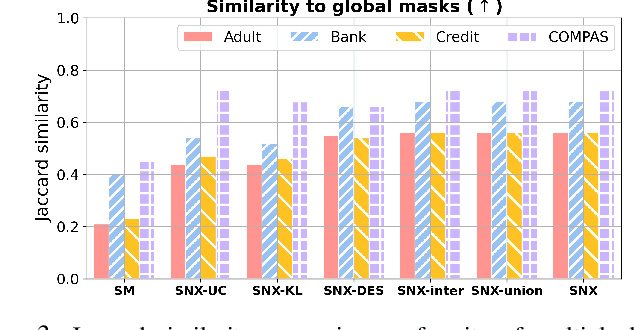
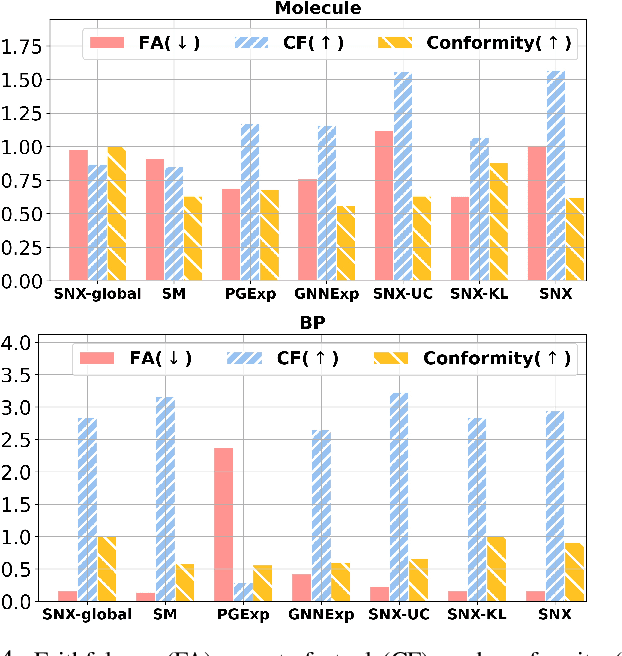
Learning to compare two objects are essential in applications, such as digital forensics, face recognition, and brain network analysis, especially when labeled data is scarce and imbalanced. As these applications make high-stake decisions and involve societal values like fairness and transparency, it is critical to explain the learned models. We aim to study post-hoc explanations of Siamese networks (SN) widely used in learning to compare. We characterize the instability of gradient-based explanations due to the additional compared object in SN, in contrast to architectures with a single input instance. We propose an optimization framework that derives global invariance from unlabeled data using self-learning to promote the stability of local explanations tailored for specific query-reference pairs. The optimization problems can be solved using gradient descent-ascent (GDA) for constrained optimization, or SGD for KL-divergence regularized unconstrained optimization, with convergence proofs, especially when the objective functions are nonconvex due to the Siamese architecture. Quantitative results and case studies on tabular and graph data from neuroscience and chemical engineering show that the framework respects the self-learned invariance while robustly optimizing the faithfulness and simplicity of the explanation. We further demonstrate the convergence of GDA experimentally.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge