SELECTOR: Selecting a Representative Benchmark Suite for Reproducible Statistical Comparison
Paper and Code
Apr 25, 2022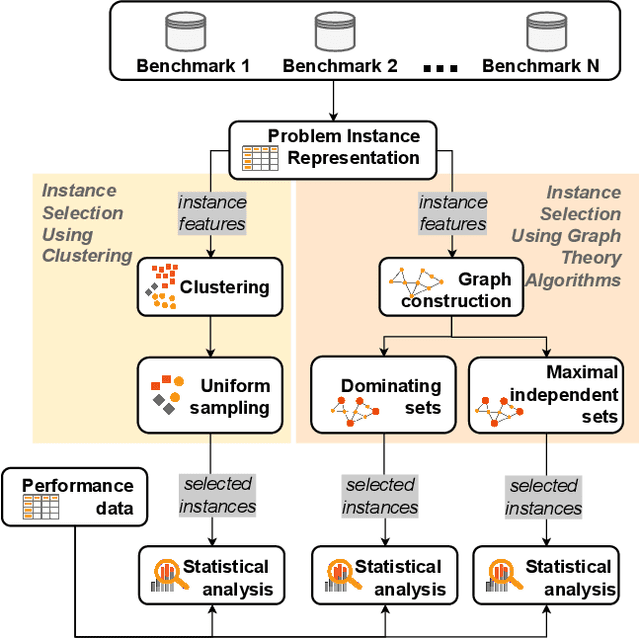

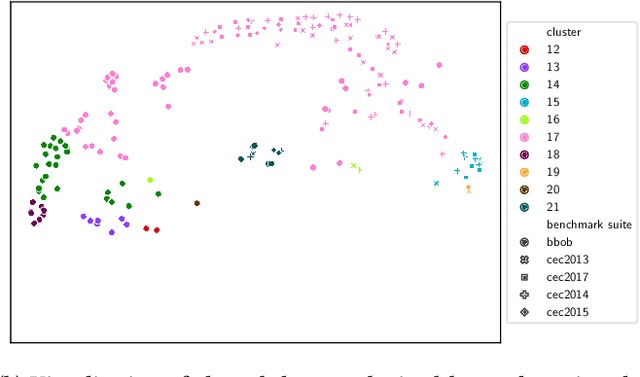
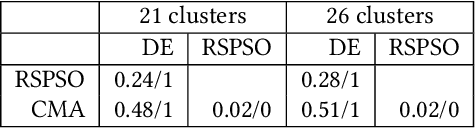
Fair algorithm evaluation is conditioned on the existence of high-quality benchmark datasets that are non-redundant and are representative of typical optimization scenarios. In this paper, we evaluate three heuristics for selecting diverse problem instances which should be involved in the comparison of optimization algorithms in order to ensure robust statistical algorithm performance analysis. The first approach employs clustering to identify similar groups of problem instances and subsequent sampling from each cluster to construct new benchmarks, while the other two approaches use graph algorithms for identifying dominating and maximal independent sets of nodes. We demonstrate the applicability of the proposed heuristics by performing a statistical performance analysis of five portfolios consisting of three optimization algorithms on five of the most commonly used optimization benchmarks. The results indicate that the statistical analyses of the algorithms' performance, conducted on each benchmark separately, produce conflicting outcomes, which can be used to give a false indication of the superiority of one algorithm over another. On the other hand, when the analysis is conducted on the problem instances selected with the proposed heuristics, which uniformly cover the problem landscape, the statistical outcomes are robust and consistent.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge