Score Matching Model for Unbounded Data Score

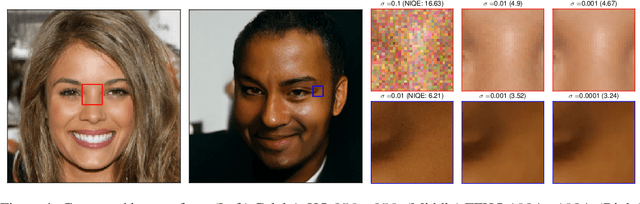
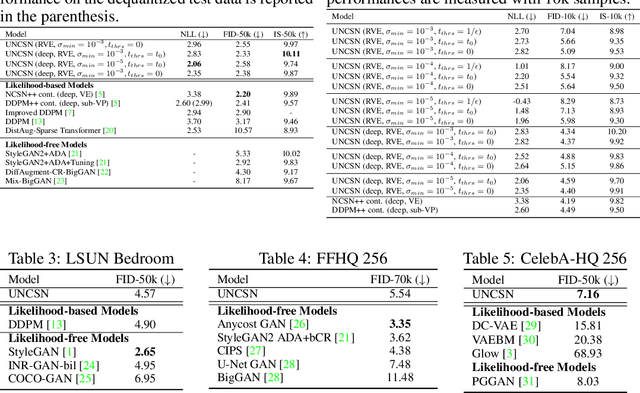
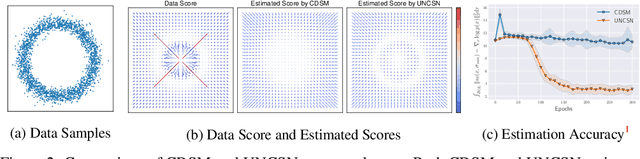
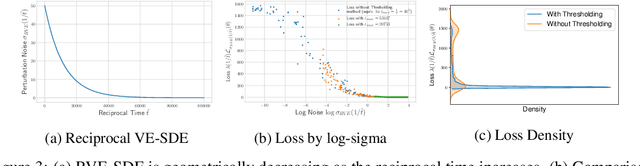
Recent advance in score-based models incorporates the stochastic differential equation (SDE), which brings the state-of-the art performance on image generation tasks. This paper improves such score-based models by analyzing the model at the zero perturbation noise. In real datasets, the score function diverges as the perturbation noise ($\sigma$) decreases to zero, and this observation leads an argument that the score estimation fails at $\sigma=0$ with any neural network structure. Subsequently, we introduce Unbounded Noise Conditional Score Network (UNCSN) that resolves the score diverging problem with an easily applicable modification to any noise conditional score-based models. Additionally, we introduce a new type of SDE, so the exact log likelihood can be calculated from the newly suggested SDE. On top of that, the associated loss function mitigates the loss imbalance issue in a mini-batch, and we present a theoretic analysis on the proposed loss to uncover the behind mechanism of the data distribution modeling by the score-based models.