Scaling the Number of Tasks in Continual Learning

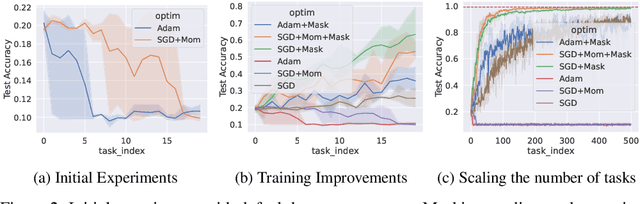
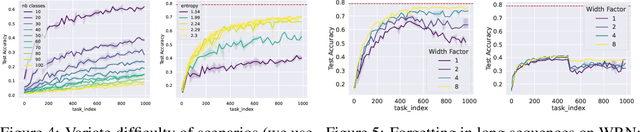
Standard gradient descent algorithms applied to sequences of tasks are known to produce catastrophic forgetting in deep neural networks. When trained on a new task in a sequence, the model updates its parameters on the current task, forgetting past knowledge. This article explores scenarios where we scale the number of tasks in a finite environment. Those scenarios are composed of a long sequence of tasks with reoccurring data. We show that in such setting, stochastic gradient descent can learn, progress, and converge to a solution that according to existing literature needs a continual learning algorithm. In other words, we show that the model performs knowledge retention and accumulation without specific memorization mechanisms. We propose a new experimentation framework, SCoLe (Scaling Continual Learning), to study the knowledge retention and accumulation of algorithms in potentially infinite sequences of tasks. To explore this setting, we performed a large number of experiments on sequences of 1,000 tasks to better understand this new family of settings. We also propose a slight modifications to the vanilla stochastic gradient descent to facilitate continual learning in this setting. The SCoLe framework represents a good simulation of practical training environments with reoccurring situations and allows the study of convergence behavior in long sequences. Our experiments show that previous results on short scenarios cannot always be extrapolated to longer scenarios.