Scalable and Efficient Continual Learning from Demonstration via Hypernetwork-generated Stable Dynamics Model
Paper and Code
Nov 06, 2023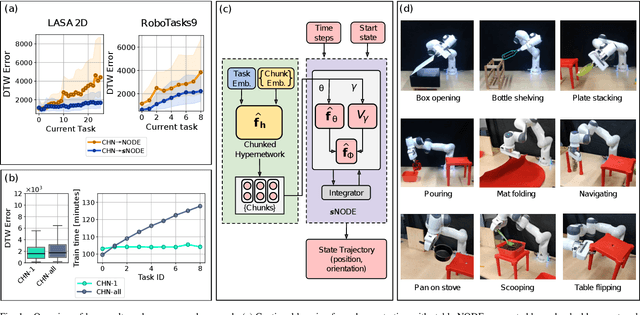
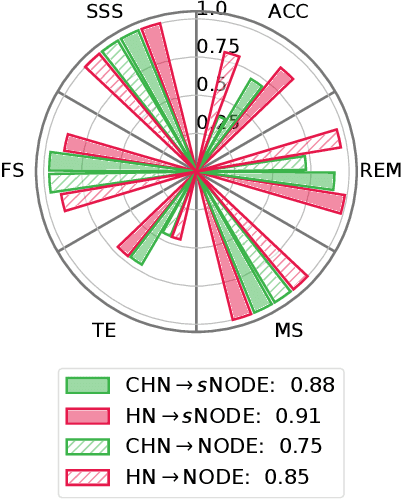
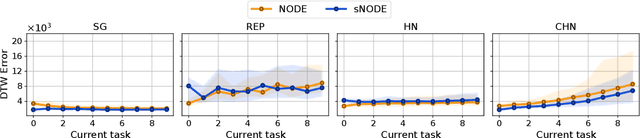
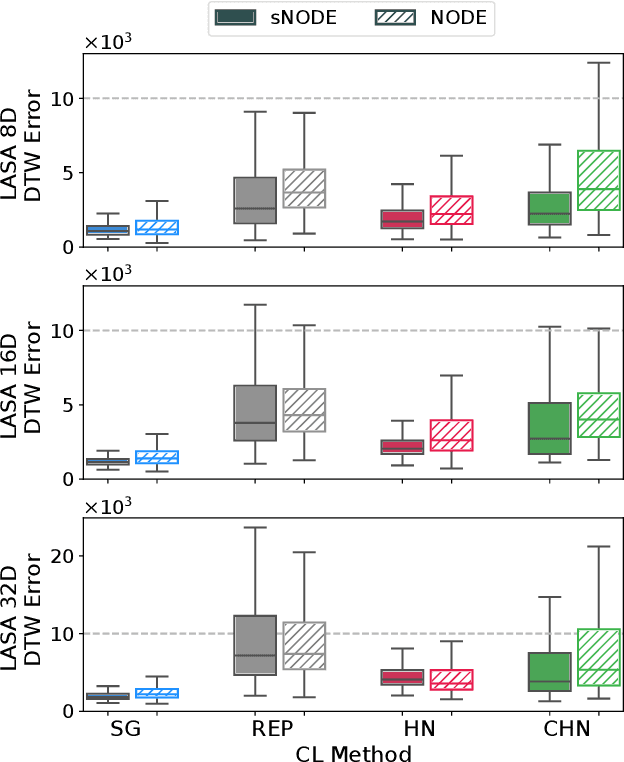
Learning from demonstration (LfD) provides an efficient way to train robots. The learned motions should be convergent and stable, but to be truly effective in the real world, LfD-capable robots should also be able to remember multiple motion skills. Multi-skill retention is a capability missing from existing stable-LfD approaches. On the other hand, recent work on continual-LfD has shown that hypernetwork-generated neural ordinary differential equation solvers, can learn multiple LfD tasks sequentially, but this approach lacks stability guarantees. We propose an approach for stable continual-LfD in which a hypernetwork generates two networks: a trajectory learning dynamics model, and a trajectory stabilizing Lyapunov function. The introduction of stability not only generates stable trajectories but also greatly improves continual learning performance, especially in the size-efficient chunked hypernetworks. With our approach, we can continually train a single model to predict the position and orientation trajectories of the robot's end-effector simultaneously for multiple real world tasks without retraining on past demonstrations. We also propose stochastic regularization with a single randomly sampled regularization term in hypernetworks, which reduces the cumulative training time cost for $N$ tasks from $\mathcal{O}(N^2)$ to $\mathcal{O}(N)$ without any loss in performance in real-world tasks. We empirically evaluate our approach on the popular LASA dataset, on high-dimensional extensions of LASA (including up to 32 dimensions) to assess scalability, and on a novel extended robotic task dataset (RoboTasks9) to assess real-world performance. In trajectory error metrics, stability metrics and continual learning metrics our approach performs favorably, compared to other baselines. Code and datasets will be shared after submission.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge