Sampling Efficient Deep Reinforcement Learning through Preference-Guided Stochastic Exploration
Paper and Code
Jun 20, 2022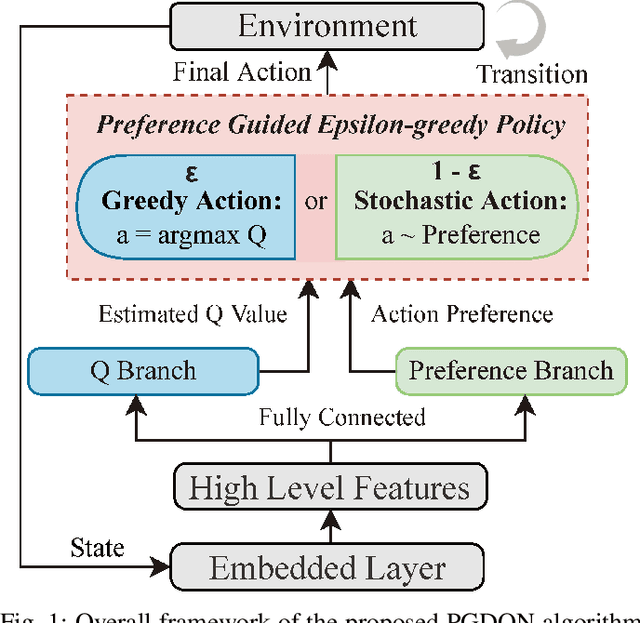
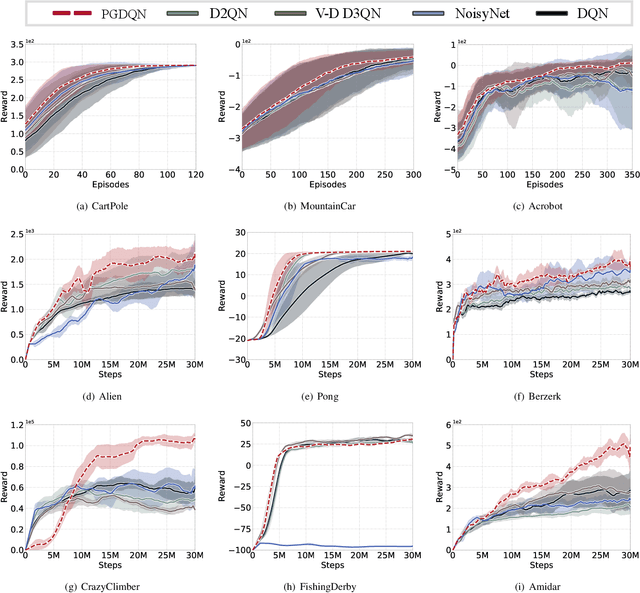
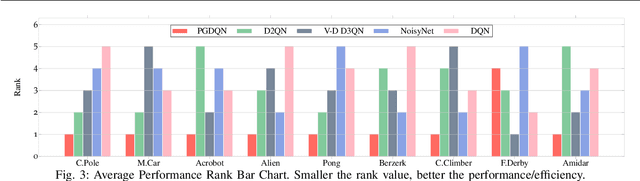
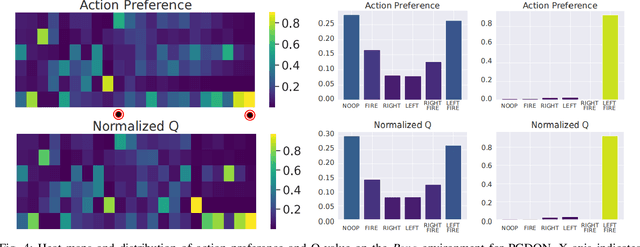
Massive practical works addressed by Deep Q-network (DQN) algorithm have indicated that stochastic policy, despite its simplicity, is the most frequently used exploration approach. However, most existing stochastic exploration approaches either explore new actions heuristically regardless of Q-values or inevitably introduce bias into the learning process to couple the sampling with Q-values. In this paper, we propose a novel preference-guided $\epsilon$-greedy exploration algorithm that can efficiently learn the action distribution in line with the landscape of Q-values for DQN without introducing additional bias. Specifically, we design a dual architecture consisting of two branches, one of which is a copy of DQN, namely the Q-branch. The other branch, which we call the preference branch, learns the action preference that the DQN implicit follows. We theoretically prove that the policy improvement theorem holds for the preference-guided $\epsilon$-greedy policy and experimentally show that the inferred action preference distribution aligns with the landscape of corresponding Q-values. Consequently, preference-guided $\epsilon$-greedy exploration motivates the DQN agent to take diverse actions, i.e., actions with larger Q-values can be sampled more frequently whereas actions with smaller Q-values still have a chance to be explored, thus encouraging the exploration. We assess the proposed method with four well-known DQN variants in nine different environments. Extensive results confirm the superiority of our proposed method in terms of performance and convergence speed. Index Terms- Preference-guided exploration, stochastic policy, data efficiency, deep reinforcement learning, deep Q-learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge