Safety-aware Policy Optimisation for Autonomous Racing
Paper and Code
Oct 14, 2021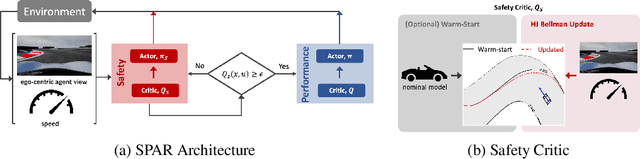
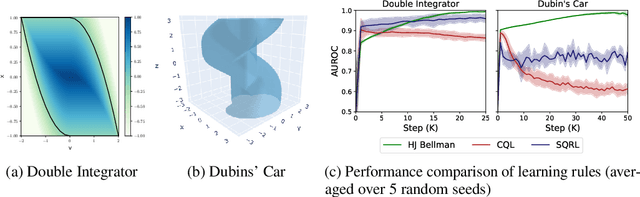
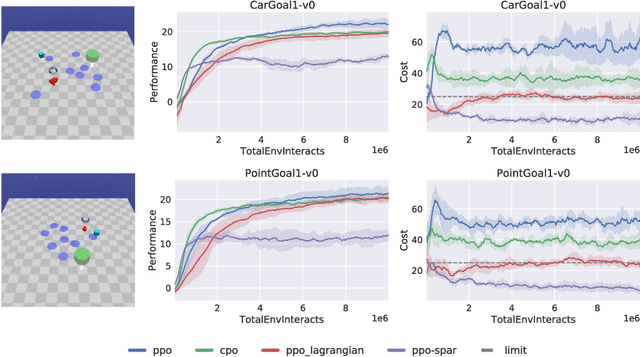

To be viable for safety-critical applications, such as autonomous driving and assistive robotics, autonomous agents should adhere to safety constraints throughout the interactions with their environments. Instead of learning about safety by collecting samples, including unsafe ones, methods such as Hamilton-Jacobi (HJ) reachability compute safe sets with theoretical guarantees using models of the system dynamics. However, HJ reachability is not scalable to high-dimensional systems, and the guarantees hinge on the quality of the model. In this work, we inject HJ reachability theory into the constrained Markov decision process (CMDP) framework, as a control-theoretical approach for safety analysis via model-free updates on state-action pairs. Furthermore, we demonstrate that the HJ safety value can be learned directly on vision context, the highest-dimensional problem studied via the method to-date. We evaluate our method on several benchmark tasks, including Safety Gym and Learn-to-Race (L2R), a recently-released high-fidelity autonomous racing environment. Our approach has significantly fewer constraint violations in comparison to other constrained RL baselines, and achieve the new state-of-the-art results on the L2R benchmark task.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge