Safe Element Screening for Submodular Function Minimization

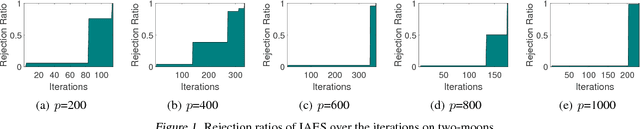
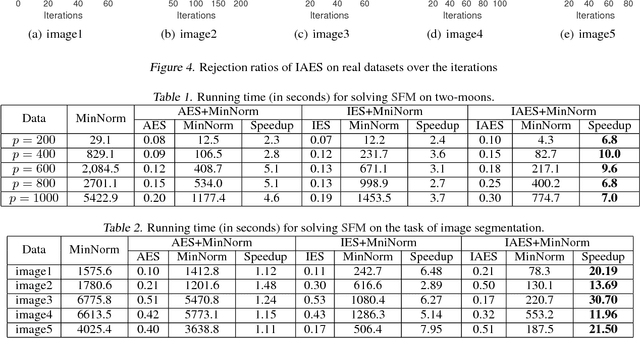
Submodular functions are discrete analogs of convex functions, which have applications in various fields, including machine learning and computer vision. However, in large-scale applications, solving Submodular Function Minimization (SFM) problems remains challenging. In this paper, we make the first attempt to extend the emerging technique named screening in large-scale sparse learning to SFM for accelerating its optimization process. We first conduct a careful studying of the relationships between SFM and the corresponding convex proximal problems, as well as the accurate primal optimum estimation of the proximal problems. Relying on this study, we subsequently propose a novel safe screening method to quickly identify the elements guaranteed to be included (we refer to them as active) or excluded (inactive) in the final optimal solution of SFM during the optimization process. By removing the inactive elements and fixing the active ones, the problem size can be dramatically reduced, leading to great savings in the computational cost without sacrificing any accuracy. To the best of our knowledge, the proposed method is the first screening method in the fields of SFM and even combinatorial optimization, thus pointing out a new direction for accelerating SFM algorithms. Experiment results on both synthetic and real datasets demonstrate the significant speedups gained by our approach.