SA-IGA: A Multiagent Reinforcement Learning Method Towards Socially Optimal Outcomes
Paper and Code
Mar 08, 2018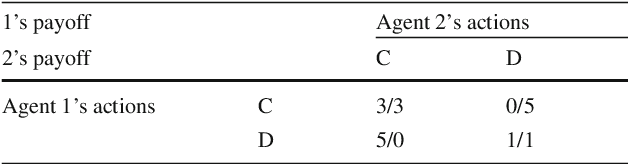


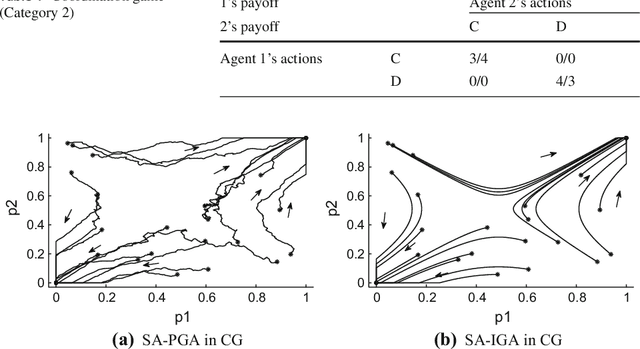
In multiagent environments, the capability of learning is important for an agent to behave appropriately in face of unknown opponents and dynamic environment. From the system designer's perspective, it is desirable if the agents can learn to coordinate towards socially optimal outcomes, while also avoiding being exploited by selfish opponents. To this end, we propose a novel gradient ascent based algorithm (SA-IGA) which augments the basic gradient-ascent algorithm by incorporating social awareness into the policy update process. We theoretically analyze the learning dynamics of SA-IGA using dynamical system theory and SA-IGA is shown to have linear dynamics for a wide range of games including symmetric games. The learning dynamics of two representative games (the prisoner's dilemma game and the coordination game) are analyzed in details. Based on the idea of SA-IGA, we further propose a practical multiagent learning algorithm, called SA-PGA, based on Q-learning update rule. Simulation results show that SA-PGA agent can achieve higher social welfare than previous social-optimality oriented Conditional Joint Action Learner (CJAL) and also is robust against individually rational opponents by reaching Nash equilibrium solutions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge