Robust parametric modeling of Alzheimer's disease progression

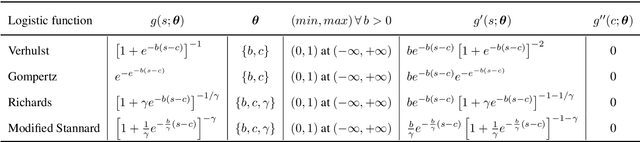
Quantitative characterization of disease progression using longitudinal data can provide long-term predictions for the pathological stages of individuals. This work studies robust modeling of Alzheimer's disease progression using parametric methods. The proposed method linearly maps individual's chronological age to a disease progression score (DPS) and robustly fits a constrained generalized logistic function to the longitudinal dynamic of a biomarker as a function of the DPS using M-estimation. Robustness of the estimates is quantified using bootstrapping via Monte Carlo resampling, and the inflection points are used to temporally order the modeled biomarkers in the disease course. Moreover, kernel density estimation is applied to the obtained DPSs for clinical status prediction using a Bayesian classifier. Different M-estimators and logistic functions, including a new generalized type proposed in this study called modified Stannard, are evaluated on the ADNI database for robust modeling of volumetric MRI and PET biomarkers, as well as neuropsychological tests. The results show that the modified Stannard function fitted using the modified Huber loss achieves the best modeling performance with a mean of median absolute errors (MMAE) of 0.059 across all biomarkers and bootstraps. In addition, applied to the ADNI test set, this model achieves a multi-class area under the ROC curve (MAUC) of 0.87 in clinical status prediction, and it significantly outperforms an analogous state-of-the-art method with a biomarker modeling MMAE of 0.059 vs. 0.061 (p < 0.001). Finally, the experiments show that the proposed model, trained using abundant ADNI data, generalizes well to data from the independent NACC database, where both modeling and diagnostic performance are significantly improved (p < 0.001) compared with using a model trained using relatively sparse NACC data.