Robust Mean Estimation under Coordinate-level Corruption

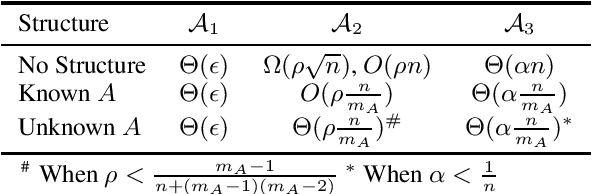
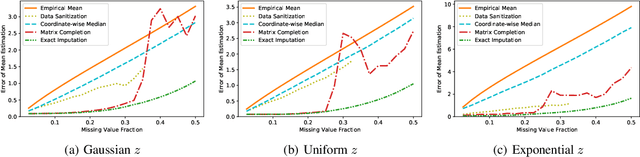
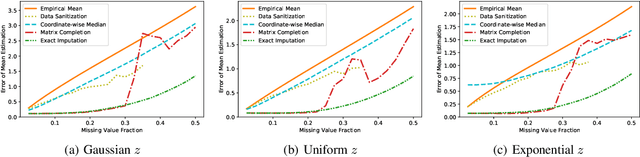
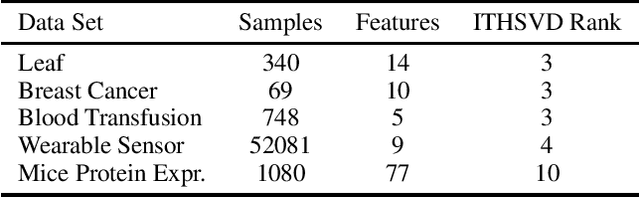
Data corruption, systematic or adversarial, may skew statistical estimation severely. Recent work provides computationally efficient estimators that nearly match the information-theoretic optimal statistic. Yet the corruption model they consider measures sample-level corruption and is not fine-grained enough for many real-world applications. In this paper, we propose a coordinate-level metric of distribution shift over high-dimensional settings with n coordinates. We introduce and analyze robust mean estimation techniques against an adversary who may hide individual coordinates of samples while being bounded by that metric. We show that for structured distribution settings, methods that leverage structure to fill in missing entries before mean estimation can improve the estimation accuracy by a factor of approximately n compared to structure-agnostic methods. We also leverage recent progress in matrix completion to obtain estimators for recovering the true mean of the samples in settings of unknown structure. We demonstrate with real-world data that our methods can capture the dependencies across attributes and provide accurate mean estimation even in high-magnitude corruption settings.