Robust Bayesian Optimization via Localized Online Conformal Prediction
Paper and Code
Nov 26, 2024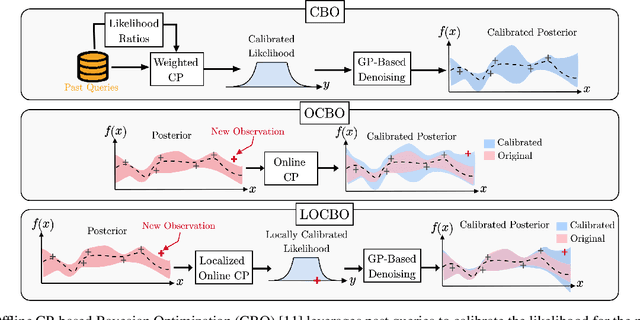
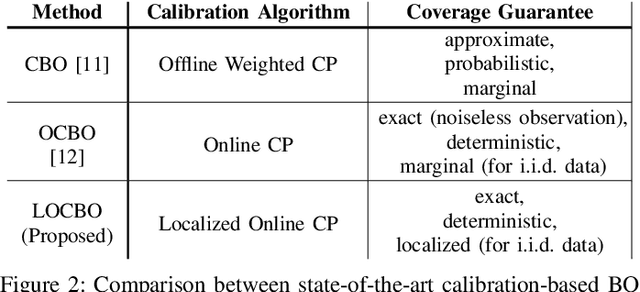
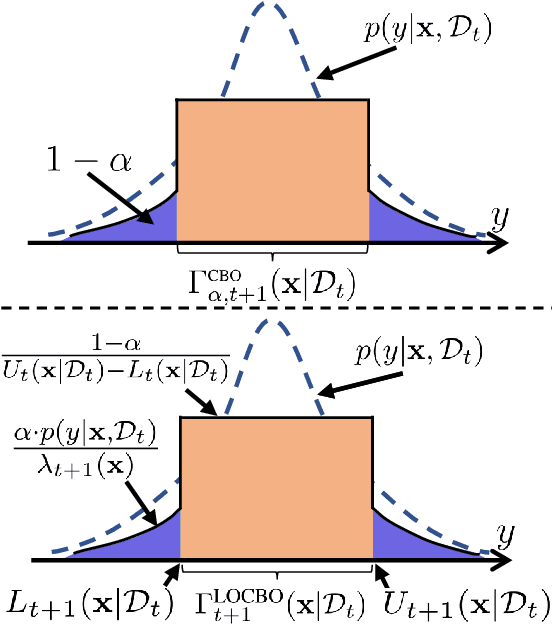
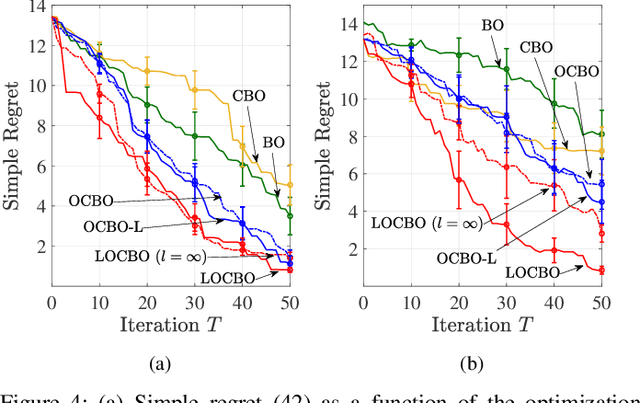
Bayesian optimization (BO) is a sequential approach for optimizing black-box objective functions using zeroth-order noisy observations. In BO, Gaussian processes (GPs) are employed as probabilistic surrogate models to estimate the objective function based on past observations, guiding the selection of future queries to maximize utility. However, the performance of BO heavily relies on the quality of these probabilistic estimates, which can deteriorate significantly under model misspecification. To address this issue, we introduce localized online conformal prediction-based Bayesian optimization (LOCBO), a BO algorithm that calibrates the GP model through localized online conformal prediction (CP). LOCBO corrects the GP likelihood based on predictive sets produced by LOCBO, and the corrected GP likelihood is then denoised to obtain a calibrated posterior distribution on the objective function. The likelihood calibration step leverages an input-dependent calibration threshold to tailor coverage guarantees to different regions of the input space. Under minimal noise assumptions, we provide theoretical performance guarantees for LOCBO's iterates that hold for the unobserved objective function. These theoretical findings are validated through experiments on synthetic and real-world optimization tasks, demonstrating that LOCBO consistently outperforms state-of-the-art BO algorithms in the presence of model misspecification.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge