Revisiting the Train Loss: an Efficient Performance Estimator for Neural Architecture Search
Paper and Code
Jun 08, 2020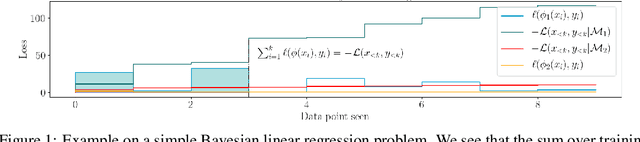
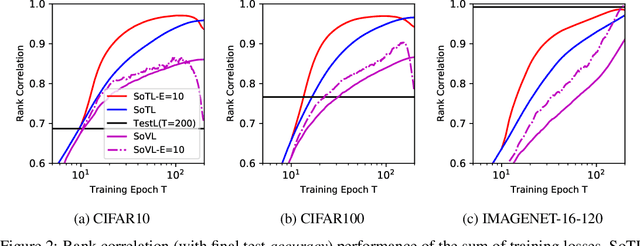
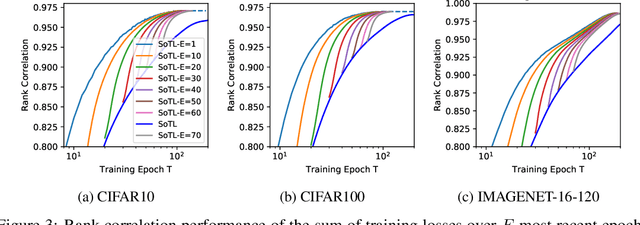
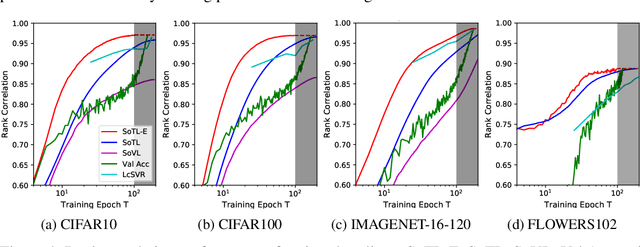
Reliable yet efficient evaluation of generalisation performance of a proposed architecture is crucial to the success of neural architecture search (NAS). Traditional approaches face a variety of limitations: training each architecture to completion is prohibitively expensive, early stopping estimates may correlate poorly with fully trained performance, and model-based estimators require large training sets. Instead, motivated by recent results linking training speed and generalisation with stochastic gradient descent, we propose to estimate the final test performance based on the sum of training losses. Our estimator is inspired by the marginal likelihood, which is used for Bayesian model selection. Our model-free estimator is simple, efficient, and cheap to implement, and does not require hyperparameter-tuning or surrogate training before deployment. We demonstrate empirically that our estimator consistently outperforms other baselines and can achieve a rank correlation of 0.95 with final test accuracy on the NAS-Bench201 dataset within 50 epochs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge