Reparameterized Variational Divergence Minimization for Stable Imitation
Paper and Code
Jun 18, 2020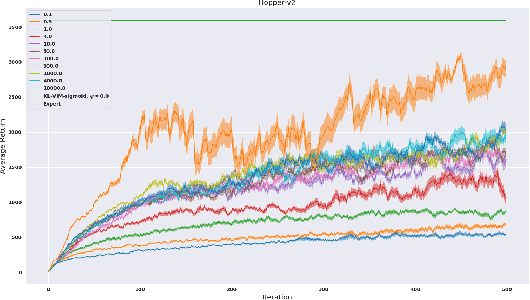

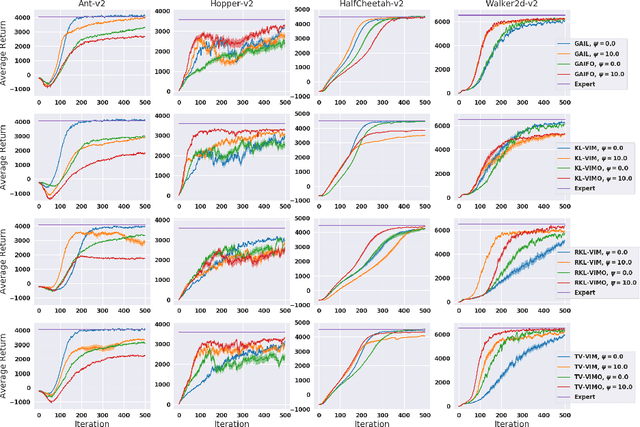
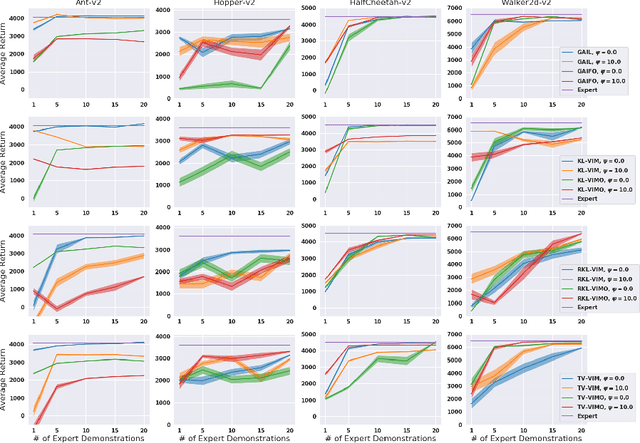
While recent state-of-the-art results for adversarial imitation-learning algorithms are encouraging, recent works exploring the imitation learning from observation (ILO) setting, where trajectories \textit{only} contain expert observations, have not been met with the same success. Inspired by recent investigations of $f$-divergence manipulation for the standard imitation learning setting(Ke et al., 2019; Ghasemipour et al., 2019), we here examine the extent to which variations in the choice of probabilistic divergence may yield more performant ILO algorithms. We unfortunately find that $f$-divergence minimization through reinforcement learning is susceptible to numerical instabilities. We contribute a reparameterization trick for adversarial imitation learning to alleviate the optimization challenges of the promising $f$-divergence minimization framework. Empirically, we demonstrate that our design choices allow for ILO algorithms that outperform baseline approaches and more closely match expert performance in low-dimensional continuous-control tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge