Reinforcement Learning with Algorithms from Probabilistic Structure Estimation
Paper and Code
Mar 15, 2021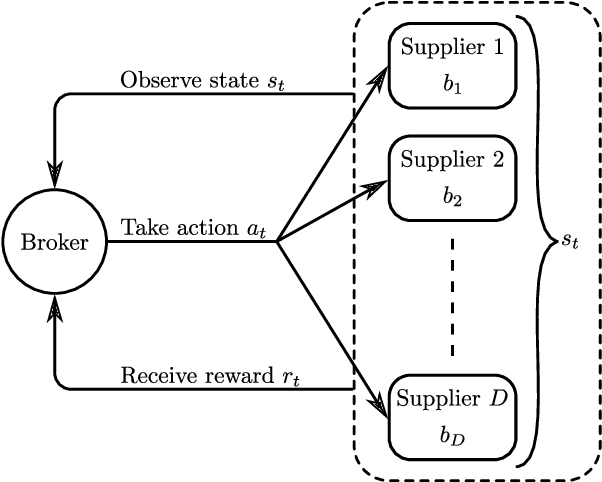
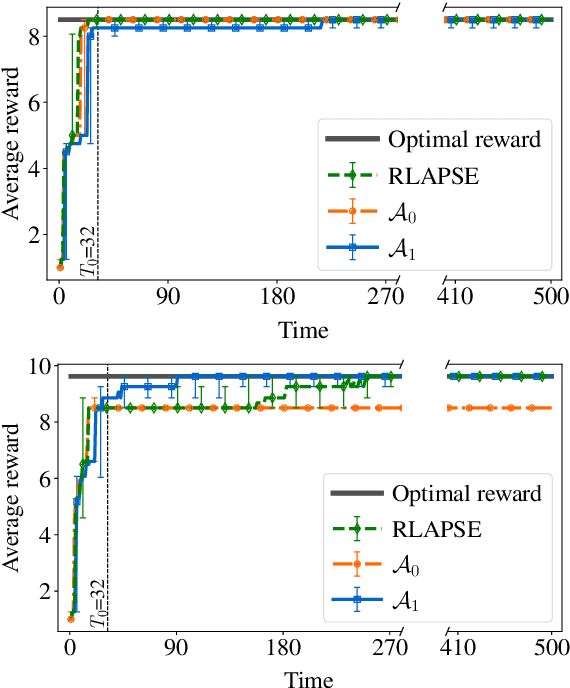
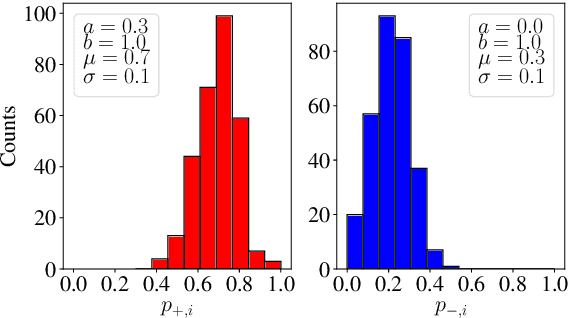
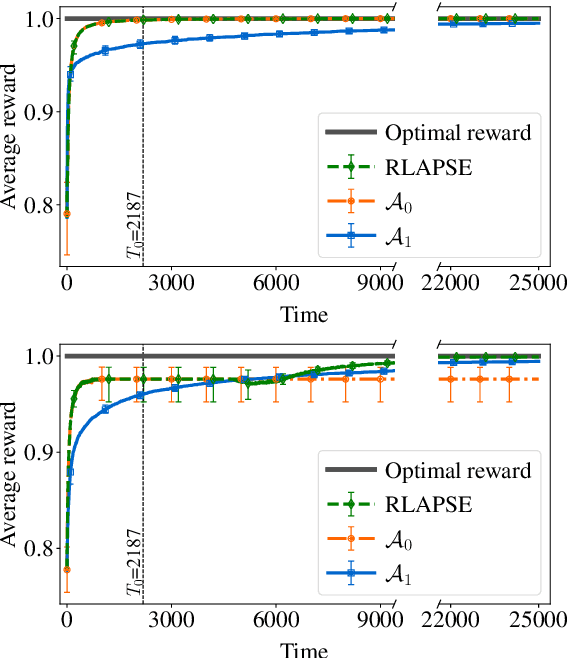
Reinforcement learning (RL) algorithms aim to learn optimal decisions in unknown environments through experience of taking actions and observing the rewards gained. In some cases, the environment is not influenced by the actions of the RL agent, in which case the problem can be modeled as a contextual multi-armed bandit and lightweight \emph{myopic} algorithms can be employed. On the other hand, when the RL agent's actions affect the environment, the problem must be modeled as a Markov decision process and more complex RL algorithms are required which take the future effects of actions into account. Moreover, in many modern RL settings, it is unknown from the outset whether or not the agent's actions will impact the environment and it is often not possible to determine which RL algorithm is most fitting. In this work, we propose to avoid this dilemma entirely and incorporate a choice mechanism into our RL framework. Rather than assuming a specific problem structure, we use a probabilistic structure estimation procedure based on a likelihood-ratio (LR) test to make a more informed selection of learning algorithm. We derive a sufficient condition under which myopic policies are optimal, present an LR test for this condition, and derive a bound on the regret of our framework. We provide examples of real-world scenarios where our framework is needed and provide extensive simulations to validate our approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge