Reinforcement Learning for Temporal Logic Control Synthesis with Probabilistic Satisfaction Guarantees
Paper and Code
Sep 11, 2019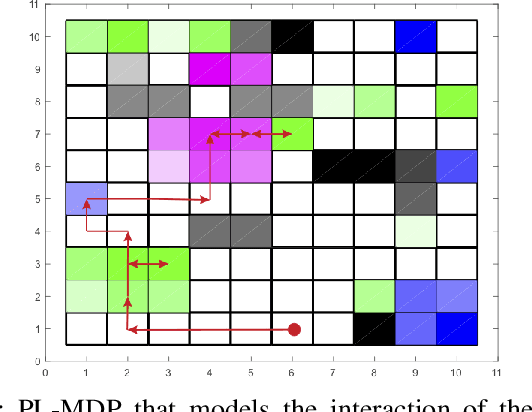

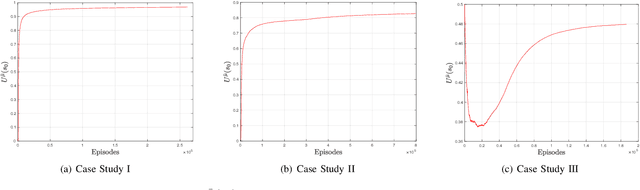
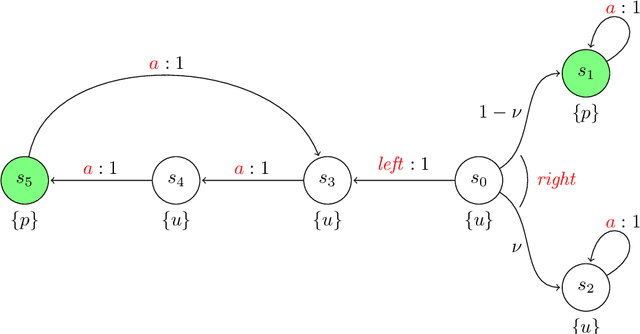
Reinforcement Learning (RL) has emerged as an efficient method of choice for solving complex sequential decision making problems in automatic control, computer science, economics, and biology. In this paper we present a model-free RL algorithm to synthesize control policies that maximize the probability of satisfying high-level control objectives given as Linear Temporal Logic (LTL) formulas. Uncertainty is considered in the workspace properties, the structure of the workspace, and the agent actions, giving rise to a Probabilistically-Labeled Markov Decision Process (PL-MDP) with unknown graph structure and stochastic behaviour, which is even more general case than a fully unknown MDP. We first translate the LTL specification into a Limit Deterministic Buchi Automaton (LDBA), which is then used in an on-the-fly product with the PL-MDP. Thereafter, we define a synchronous reward function based on the acceptance condition of the LDBA. Finally, we show that the RL algorithm delivers a policy that maximizes the satisfaction probability asymptotically. We provide experimental results that showcase the efficiency of the proposed method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge