Regret Bounds for Kernel-Based Reinforcement Learning
Paper and Code
Apr 12, 2020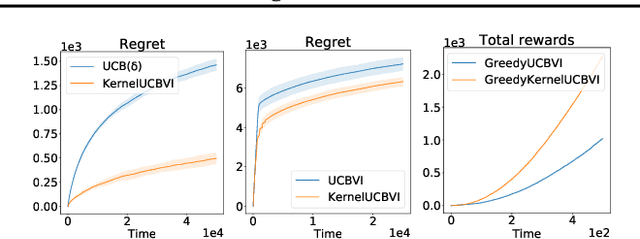

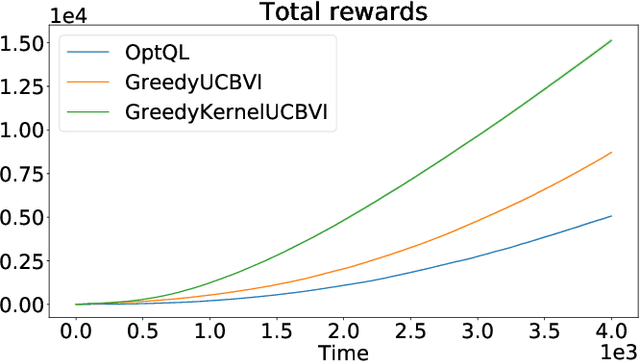
We consider the exploration-exploitation dilemma in finite-horizon reinforcement learning problems whose state-action space is endowed with a metric. We introduce Kernel-UCBVI, a model-based optimistic algorithm that leverages the smoothness of the MDP and a non-parametric kernel estimator of the rewards and transitions to efficiently balance exploration and exploitation. Unlike existing approaches with regret guarantees, it does not use any kind of partitioning of the state-action space. For problems with $K$ episodes and horizon $H$, we provide a regret bound of $O\left( H^3 K^{\max\left(\frac{1}{2}, \frac{2d}{2d+1}\right)}\right)$, where $d$ is the covering dimension of the joint state-action space. We empirically validate Kernel-UCBVI on discrete and continuous MDPs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge