Reducing the variance in online optimization by transporting past gradients

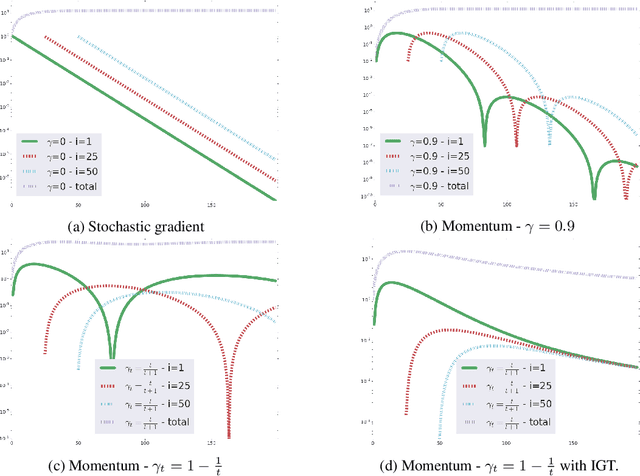
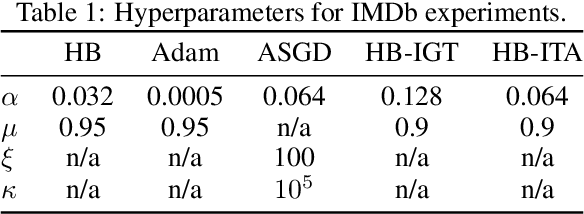
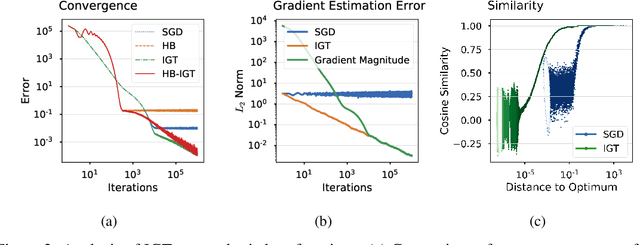
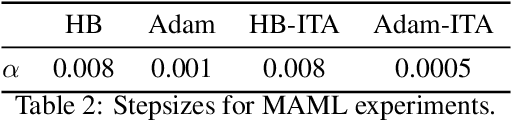
Most stochastic optimization methods use gradients once before discarding them. While variance reduction methods have shown that reusing past gradients can be beneficial when there is a finite number of datapoints, they do not easily extend to the online setting. One issue is the staleness due to using past gradients. We propose to correct this staleness using the idea of implicit gradient transport (IGT) which transforms gradients computed at previous iterates into gradients evaluated at the current iterate without using the Hessian explicitly. In addition to reducing the variance and bias of our updates over time, IGT can be used as a drop-in replacement for the gradient estimate in a number of well-understood methods such as heavy ball or Adam. We show experimentally that it achieves state-of-the-art results on a wide range of architectures and benchmarks. Additionally, the IGT gradient estimator yields the optimal asymptotic convergence rate for online stochastic optimization in the restricted setting where the Hessians of all component functions are equal.