Rapid Convex Optimization of Centroidal Dynamics using Block Coordinate Descent
Paper and Code
Aug 04, 2021
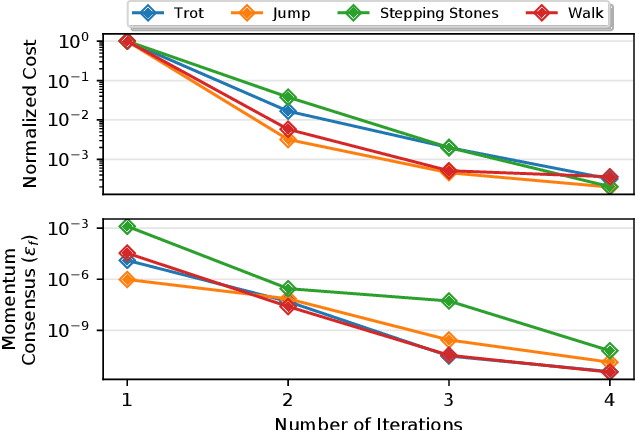
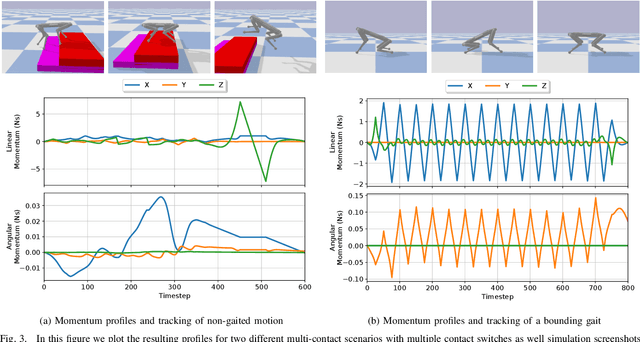
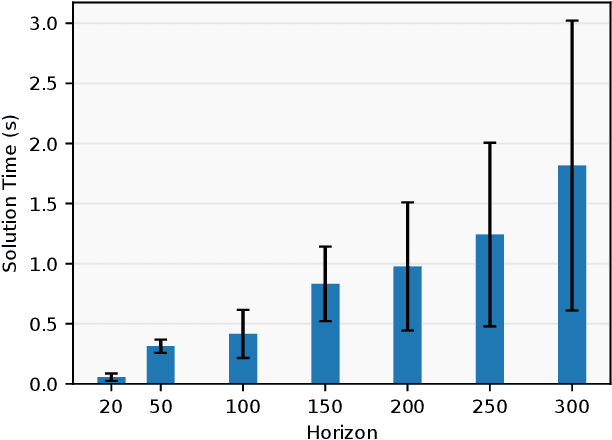
In this paper we explore the use of block coordinate descent (BCD) to optimize the centroidal momentum dynamics for dynamically consistent multi-contact behaviors. The centroidal dynamics have recently received a large amount of attention in order to create physically realizable motions for robots with hands and feet while being computationally more tractable than full rigid body dynamics models. Our contribution lies in exploiting the structure of the dynamics in order to simplify the original non-convex problem into two convex subproblems. We iterate between these two subproblems for a set number of iterations or until a consensus is reached. We explore the properties of the proposed optimization method for the centroidal dynamics and verify in simulation that motions generated by our approach can be tracked by the quadruped Solo12. In addition, we compare our method to a recently proposed convexification using a sequence of convex relaxations as well as a more standard interior point method used in the off- the-shelf solver IPOPT to show that our approach finds similar, if not better, trajectories (in terms of cost), and is more than four times faster than both approaches. Finally, compared to previous approaches, we note its practicality due to the convex nature of each subproblem which allows our method to be used with any off-the-shelf quadratic programming solver.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge