Projected Sliced Wasserstein Autoencoder-based Hyperspectral Images Anomaly Detection
Paper and Code
Dec 22, 2021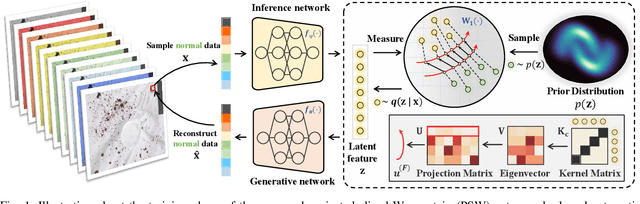

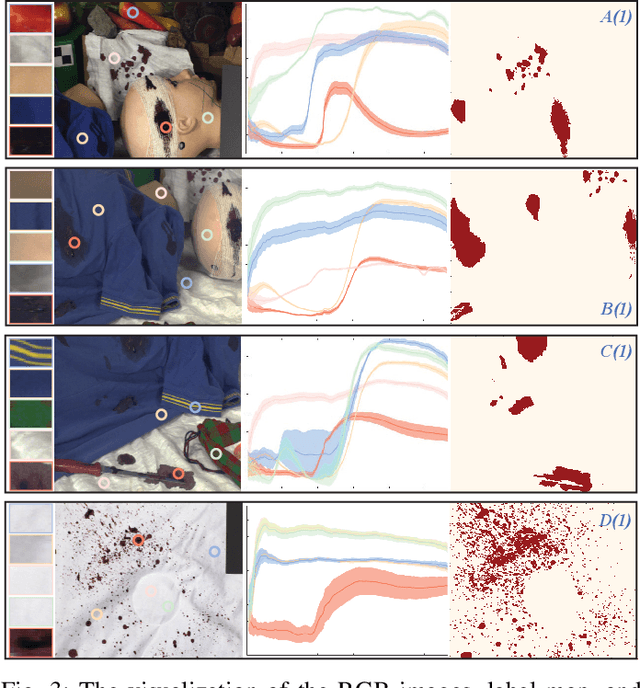
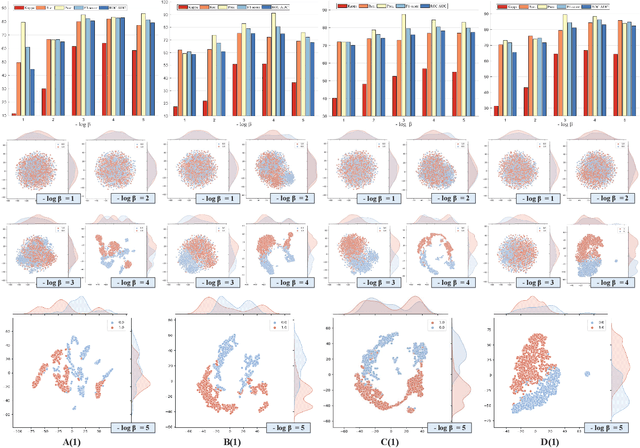
Anomaly detection (AD) has been an active research area in various domains. Yet, the increasing data scale, complexity, and dimension turn the traditional methods into challenging. Recently, the deep generative model, such as the variational autoencoder (VAE), has sparked a renewed interest in the AD problem. However, the probability distribution divergence used as the regularization is too strong, which causes the model cannot capture the manifold of the true data. In this paper, we propose the Projected Sliced Wasserstein (PSW) autoencoder-based anomaly detection method. Rooted in the optimal transportation, the PSW distance is a weaker distribution measure compared with $f$-divergence. In particular, the computation-friendly eigen-decomposition method is leveraged to find the principal component for slicing the high-dimensional data. In this case, the Wasserstein distance can be calculated with the closed-form, even the prior distribution is not Gaussian. Comprehensive experiments conducted on various real-world hyperspectral anomaly detection benchmarks demonstrate the superior performance of the proposed method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge