Progressive Identification of True Labels for Partial-Label Learning
Paper and Code
Feb 19, 2020

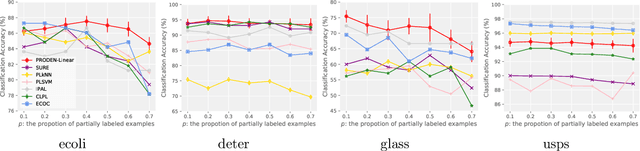
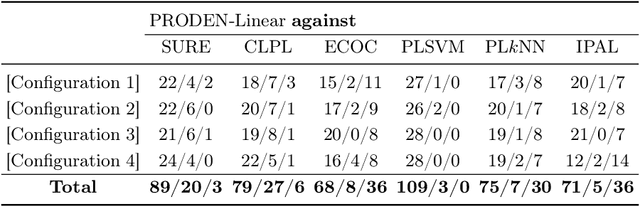
Partial-label learning is one of the important weakly supervised learning problems, where each training example is equipped with a set of candidate labels that contains the true label. Most existing methods elaborately designed learning objectives as constrained optimizations that must be solved in specific manners, making their computational complexity a bottleneck for scaling up to big data. The goal of this paper is to propose a novel framework of partial-label learning without implicit assumptions on the model or optimization algorithm. More specifically, we propose a general estimator of the classification risk, theoretically analyze the classifier-consistency, and establish an estimation error bound. We then explore a progressive identification method for approximately minimizing the proposed risk estimator, where the update of the model and identification of true labels are conducted in a seamless manner. The resulting algorithm is model-independent and loss-independent, and compatible with stochastic optimization. Thorough experiments demonstrate it sets the new state of the art.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge