Probabilistic Feature Selection and Classification Vector Machine
Paper and Code
Jun 13, 2018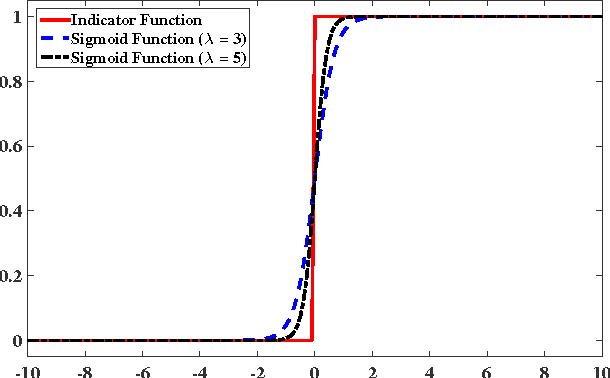
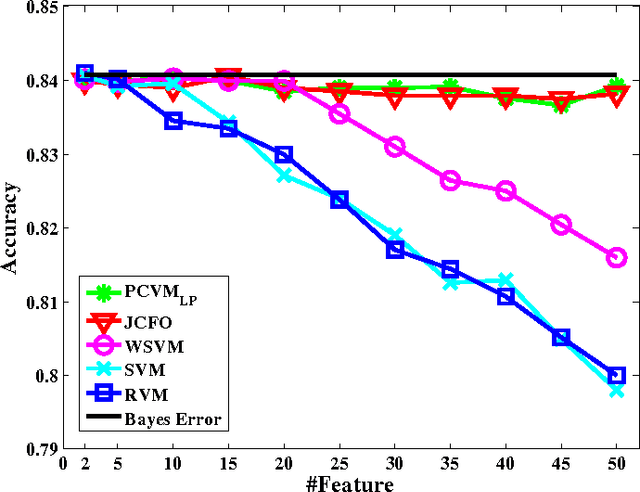
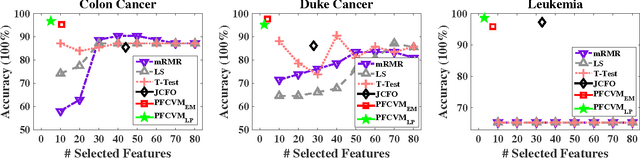
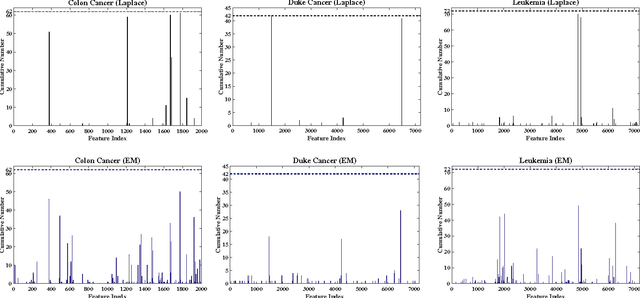
Sparse Bayesian learning is a state-of-the-art supervised learning algorithm that can choose a subset of relevant samples from the input data and make reliable probabilistic predictions. However, in the presence of high-dimensional data with irrelevant features, traditional sparse Bayesian classifiers suffer from performance degradation and low efficiency by failing to eliminate irrelevant features. To tackle this problem, we propose a novel sparse Bayesian embedded feature selection method that adopts truncated Gaussian distributions as both sample and feature priors. The proposed method, called probabilistic feature selection and classification vector machine (PFCVMLP ), is able to simultaneously select relevant features and samples for classification tasks. In order to derive the analytical solutions, Laplace approximation is applied to compute approximate posteriors and marginal likelihoods. Finally, parameters and hyperparameters are optimized by the type-II maximum likelihood method. Experiments on three datasets validate the performance of PFCVMLP along two dimensions: classification performance and effectiveness for feature selection. Finally, we analyze the generalization performance and derive a generalization error bound for PFCVMLP . By tightening the bound, the importance of feature selection is demonstrated.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge